Hi Peter,
I have tried to evaluate the anti derivative i.e. integration of the function you have supplied.The result is the following.
In[1] = Integrate[(24 - 10 Sin[x] + (Sin[x])^2)/(6 - 5 Sin[x] + (Sin[x])^2),x]
Out[1] = x + (3 ArcTan[(1 - 3 Tan[x/2])/(2 Sqrt[2])])/Sqrt[2] -16 ArcTan[(1 - 2 Tan[x/2])/Sqrt[3]])/Sqrt[3]
It works fine. Perhaps you did not use the syntax properly.
The plot what I have got is,
Plot[x + (3 ArcTan[(1 - 3 Tan[x/2])/(2 Sqrt[2])])/Sqrt[2] - (16 ArcTan[(1 - 2 Tan[x/2])/Sqrt[3]])/Sqrt[3], {x, -8, 8}]
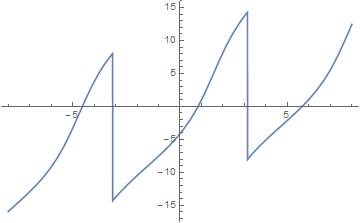
Suvadip