Hi everyone,
I'm trying to solve the heat equation with the finite elements method using mathematica 10 but I got some issues:/
Here's my problem
My working space is a box 100x40x100. I got a heat source which is a finite semi cylinder: -3<x<3 and y^2+z^2 <= 1 and z => 0 this source has a temperature which varies with time the flow of the heat is 0 on the borders of my working space and my source of heat. I want to modelize the heat in my box over time.
So first I tried to solve this equation with a constant source of temperature: T=300
Thus I typed the following code:
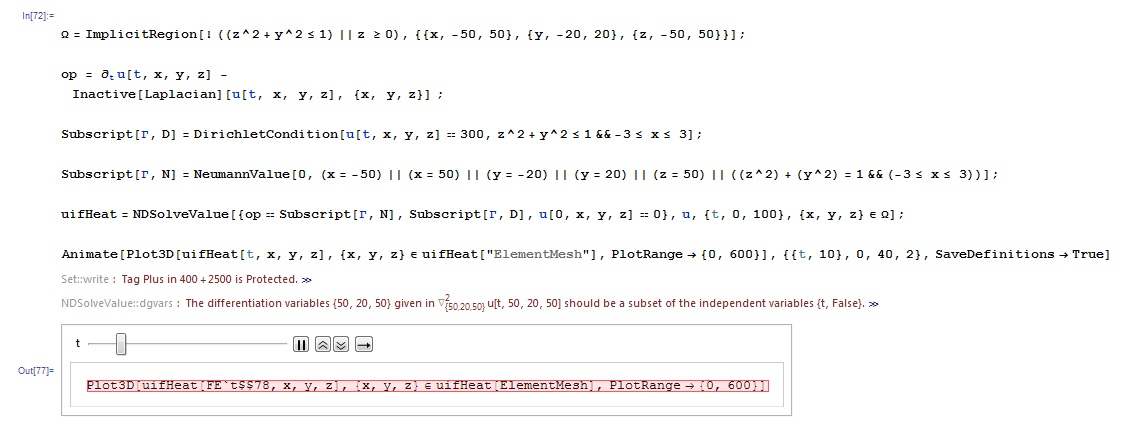
\[CapitalOmega] =
ImplicitRegion[! ((z^2 + y^2 <= 1) || z <= 0), {{x, -50,
50}, {y, -20, 20}, {z, -50, 50}}]; -> creation of my working space, which the whole box except the semi cylinder
op = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(u[t, x, y, z]\)\) -
Inactive[Laplacian][u[t, x, y, z], {x, y, z}] ; -> writting of the heat equation
Subscript[\[CapitalGamma], D] =
DirichletCondition[u[t, x, y, z] == 300,
z^2 + y^2 <= 1 && -3 <= x <= 3]; -> I'm setting up my initial conditions: a constant temperature on my semi cylinder
Subscript[\[CapitalGamma], N] =
NeumannValue[
0, (x = -50) || (x = 50) || (y = -20) || (y = 20) || (z =
50) || ((z^2) + (y^2) = 1 && (-3 <= x <= 3))]; -> I want the heat flow = 0 on the borders of my box and the semi cylinder ( heat must not
escape from my box)
uifHeat =
NDSolveValue[{op == Subscript[\[CapitalGamma], N],
Subscript[\[CapitalGamma], D], u[0, x, y, z] == 0},
u, {t, 0, 100}, {x, y, z} \[Element] \[CapitalOmega]]; -> I'm solving the equation
Animate[Plot3D[
uifHeat[t, x, y, z], {x, y, z} \[Element] uifHeat["ElementMesh"],
PlotRange -> {0, 600}], {{t, 10}, 0, 40, 2},
SaveDefinitions -> True] -> plotting of the solution
But I got some error messages and I don't understand where my mistakes are

The first one obviously comes from my definition of neumann value with the (z^2+y^2<1) border but I don't understand what is the matter. The second one seems to be due to the fact that x, y and z are no longer variables but figures at the end of my code but I can't see where is my mistake.
Does anyone has an idea of what I should correct?
Here is a picture of my code:
PS: English is not my native language so I'm sorry for my grammar mistakes xp