Since the MRB constant is
Sum[(-1)^n (n^(1/n) - 1), {n, 1, Infinity}],
it got me wondering what the divergent
Sum[(I)^n (n^(1/n) - I), {n, 1, Infinity}],
where I is the imaginary unit in 2 places above, does.
I found out the sum has 4 accumulation points.
Here is how I deduced that:
l = N[Accumulate[Table[(I)^k (k^(1/k) - I), {k, 100}]]];
ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ l, AspectRatio -> 1]
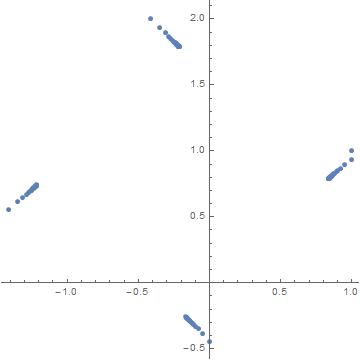
In[24]:= Table[l[[-x]], {x, 1, 4}]
Out[24]= {-0.165382 - 0.258948 I, -1.21251 + 0.741052 I, -0.21251 +
1.78856 I, 0.835387 + 0.788561 I}
In[25]:= l = N[Accumulate[Table[(I)^k (k^(1/k) - I), {k, 1000}]]];
In[26]:= ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ l,
AspectRatio -> 1]
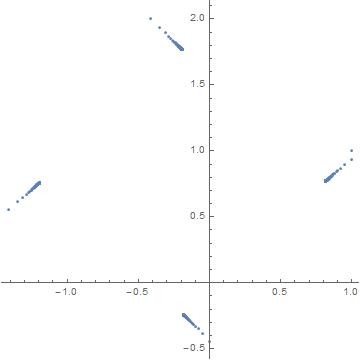
In[27]:= Table[l[[-x]], {x, 1, 4}]
Out[27]= {-0.185294 - 0.238851 I, -1.19223 + 0.761149 I, -0.192226 +
1.76809 I, 0.814718 + 0.768086 I}
In[28]:= l = N[Accumulate[Table[(I)^k (k^(1/k) - I), {k, 10000}]]];
In[29]:= ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ l,
AspectRatio -> 1]
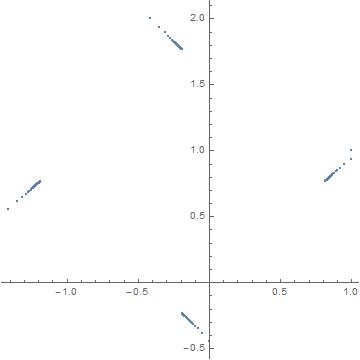
In[30]:= Table[l[[-x]], {x, 1, 4}]
Out[30]= {-0.188296 - 0.235846 I, -1.18922 + 0.764154 I, -0.189218 +
1.76508 I, 0.811704 + 0.765075 I}
In[39]:= -0.18829645859705124` -
0.23584620227704534` I - (-1.189217916916732` + 0.7641537977229609` I)
Out[39]= 1.00092 - 1. I
In[40]:= -0.18921791691673207` +
1.7650753382290296` I - (0.8117037057913876` + 0.7650753382290443` I)
Out[40]= -1.00092 + 1. I
In[41]:= -1.189217916916732` +
0.7641537977229609` I - (-0.18921791691673207` +
1.7650753382290296` I)
Out[41]= -1. - 1.00092 I,
where the 1.00092 either eventually goes to 1 as n goes to infinity or it could be a separate (probably new) constant that the accumulation points differ by.