Hi everyone,
I'm trying to compute the following definite integral (Mu is a parameter):
Integrate[Sqrt[3]/Sqrt[1 + Sqrt[1 + 12*u^2 - 24*\[Mu]]], {u, -Sqrt[1 + 8*\[Mu]]/2, Sqrt[1 + 8*\[Mu]]/2}]
Only for some specific case of Mu Mathematica seems to be able to compute it. The "funny" things are that:
- if I keep the integral indefinite, it returns me a solution (quite ugly, but at least...):
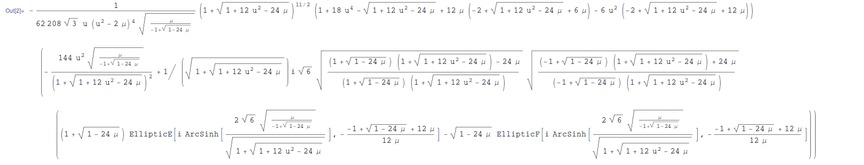
- if I give precise values for the boundary (e.g, u=+-1/2), after a long time it just returns the definite integral without any result.
- if I additionally specify a precise value of Mu (so it knows Mu + boundary of integration), in one lucky case it is able to directly give me the result for the definite integral; this does not match with the value I would obtain by using the fundamental theorem of calculus (i.e. substituting the values of Mu and u in the ugly formula and taking the difference).
Has any of you an idea about what the problem could be? I would like to also point out that the square roots are always well definite for the values I consider.
Thank you.