I think there may be two bugs in the VertexContract function:
1) The updated graph does not include reasonable edgeweights 2) The function does not actually reduce the number of vertices in the graph. If I have n vertices, and I merge m of them, I would expect to have n-m+1 vertex after the operation.
Let me run through a simple example. In the following a simple graph is built:
gr = { {"a" \[DirectedEdge] "b", 1000}, {"b" \[DirectedEdge] "c", 2000}, {"c" \[DirectedEdge] "d", 3000}, {"d" \[DirectedEdge] "a", 4000}}
test1 = Graph[ (First[#]) & /@ gr, VertexLabels -> "Name", EdgeWeight -> (Last[#] & /@ gr), EdgeLabels -> "EdgeWeight"]
The graph, then, is 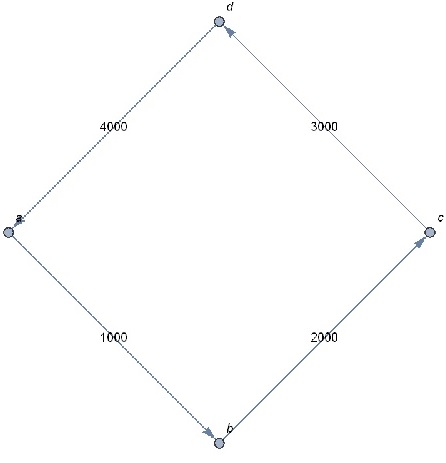
I now wish to merge vertices a and b:
test2 = VertexContract[test1, {"a", "b"}]
which yields a graph that has the correct structure, but the EdgeWeight information is magically gone (even on the c -> d edge that is not modified), and has been replaced with 1. Also, note the orphaned node in the bottom corner:

To confirm:
Normal[WeightedAdjacencyMatrix[test2] ]
Yields
{{0, 1, 0, 0}, {0, 0, 0, 1}, {0, 0, 0, 0}, {1, 0, 0, 0}}
whereas the original had the correct values:
{{0, 1000, 0, 0}, {0, 0, 2000, 0}, {0, 0, 0, 3000}, {4000, 0, 0, 0}}
Clearly showing that: - There is one vertex too many: There should be three, but there are 4 (including a phantom one with all 0's in the weights) - The weights are all reduced to 1 for some reason If I use the VertexList function to get the vertices of the updated graph I get
{"c", "d", "a", 1}
There seems to be a phantom node lying around. I had expected a list with the elements {"c", "d", 1}.
I am new to this area, so I will exercise some humility and ask if this is a bug, or my expectations that are wrong? Is the new vertex always added as the last one in the vertex list? Are there workarounds that do not lose the weights?