Using the substitution $u'(x)=v(u(x))$ which results in $u''(x)=v'(u)u'(x)$ or $u''(x)=v'(u)v(u)$. Plugging these in the ode result in a first order nonlinear ode in $v(u)$ which is $v'(u)+\frac{u}{v(u)}-\frac{u^3}{v(u)}=0$ which can now be solved for $v(u)$. Now use this solution to solve for the first oder order ode $u'(x)=v(u(x))$. The problem is with the boundary conditions at $\pm \infty$. btw, you had them reversed.

I had to sneek in a simpler boundary conditions at zero.

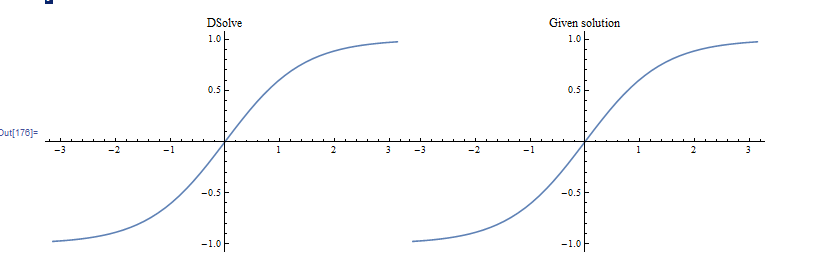
The solution is in terms of inverse function with logs, which you can try to convert to trig. But I plotted it and it does match the $\frac{\tanh(x)}{\sqrt{2}}$. I only used one of the 2 solutions here.

Clear[u, v, x];
eq = v'[u] + u/v[u] - u^3/v[u] == 0;
sol = v[u] /. First@DSolve[{eq, v[0] == 1/Sqrt[2]}, v[u], u];
sol = u[x] /. First@DSolve[{u'[x] == (sol /. u -> u[x]), u[0] == 0}, u[x], x]

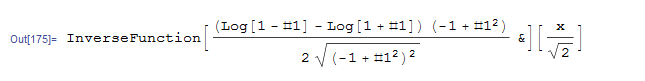
Plotting it side-by-side to the proposed solution shows it is the same

Row[{
  Plot[sol /. x -> t, {t, -Pi, Pi}, ImageSize -> Medium, PlotLabel -> "DSolve"],
  Plot[Tanh[x/Sqrt[2]], {x, -Pi, Pi}, ImageSize -> Medium, PlotLabel -> "Given solution"]}
 ]

Any tip on how can I solve $v?(u)+\frac{u}{v(u)}?\frac{u^3}{v(u)}=0$ analytically?

This is separable, so direct integration solves it. Since $v'(u)=f(v,u)$ can be written as $v'(u)= \frac{-1}{v} (u-u^3)$ so it is separable. Rearranging gives $v v'(u) = u^3-u$ or $v \frac{dv}{du}=u^3-u$ now integrating both sides gives $\int vdv=\int (u^3-u)du$ or $\frac{v^2}{2}=\frac{u^4}{4}-\frac{u^2}{2}+c$. Using the initial condition that $v(0)=\frac{1}{\sqrt{2}}$ gives $c=\frac{1}{4}$, plugging this back and simplifying gives $v(u)=\frac{\sqrt{(u^2-1)^2}}{\sqrt{2}}$ which is what Mathematica gives.