Group Abstract Group Abstract

Message Boards Message Boards

0
|
4.5K Views
|
2 Replies
|
1 Total Like
View groups...
Share
Share this post:

Is it possible to plot a piece-wise function with variable bounds?

Alec Thomson
Posted 11 years ago

Specifically I am trying to plot the following:

Equation

As v_r vs. l, sampling d in digit intervals from d=5 to d=15. Please forgive the specific nature of this question but I am having trouble finding a solution. The domain of l only need be 0 to pi/2.

For the sake of context here is the rest of my visualisation:

Plot[{Evaluate[
   Table[Sin[l]*(2500/Sqrt[100 + d^2 - 20*d*Cos[l]] - 250), {d, 0, 
     5}]], Evaluate[
   Table[Sin[l]*(2500/Sqrt[100 + d^2 - 20*d*Cos[l]] - 250), {d, 15, 
     20}]]}, {l, 0, \[Pi]/2}, AxesLabel -> {l, v}]

Graph

I have tried using a combination of the Table and Piecewise functions, but to no avail. I would greatly appreciate any help.

Cheers.
POSTED BY: Alec Thomson
2 Replies
Sort By:

Sometimes an alternative to Piecewise is a construction something like

f[x_]:=f1[x] Boole[condition1]+f2[x] Boole[condition2]
POSTED BY: S M Blinder
Kuba Podkalicki
Kuba Podkalicki
Posted 11 years ago

Quick answer:

Evaluate @ Table[
  Sin[l] Piecewise[{
     {250, 0 < l < ArcCos[(d^2 + 75)/(20 d)]},
     {2500/Sqrt[100 + d^2 - 20 d Cos[l]] - 250,   l > ArcCos[(d^2 + 75)/(20 d)]}}],
  {d, 5, 15, 2}]

Basic answer:

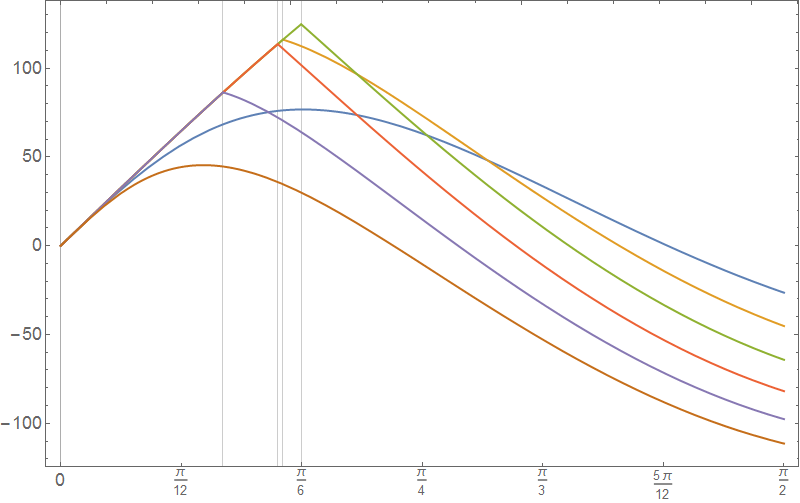
Plot[     Evaluate@ Table[Sin[  l] Piecewise[{{250,   0 < l < ArcCos[(d^2 + 75)/(20 d)]}, {2500/   Sqrt[100 + d^2 - 20 d Cos[l]] - 250, 
       l > ArcCos[(d^2 + 75)/(20 d)]}}], {d, 5, 15, 2}],
 {l, 0, Pi/2},
 PlotRange -> All, ImageSize -> 800, Axes -> False, Frame -> True,
 FrameTicks -> {{Automatic, Automatic}, {Range[0, Pi/2, Pi/12],     Automatic}},
 GridLines -> {Table[ArcCos[(d^2 + 75.)/(20 d)], {d, 5, 15, 2}], {}},   PlotStyle -> Thick, BaseStyle -> 18]

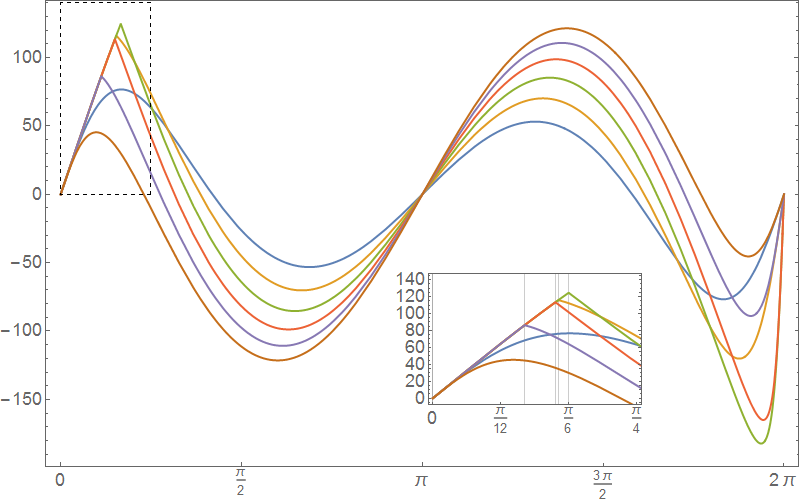
enter image description here Extended answer:

Plot[   Evaluate@Table[    Sin[l] Piecewise[{  {250, 0 < l < ArcCos[(d^2 + 75)/(20 d)]},
       {2500/Sqrt[100 + d^2 - 20 d Cos[l]] - 250,   l > ArcCos[(d^2 + 75)/(20 d)]}}],   {d, 5, 15, 2}],
  {l, 0, 2 Pi},
  PlotRange -> All, ImageSize -> 800, Axes -> False, Frame -> True,
  FrameTicks -> {{Automatic, Automatic}, {Range[0, 2 Pi, Pi/2], None}},
  PlotStyle -> Thick,    BaseStyle -> 18
  ] //  Show[#, Epilog -> {    {EdgeForm@Dashed, FaceForm@None, Rectangle[{0, 0}, {Pi/4, 140}]},
           Inset[
            Show[#, PlotRange -> {{0, Pi/4}, {0, 140}}, ImageSize -> 250, 
             FrameTicks -> {{Automatic, Automatic}, {Range[0, Pi/4, Pi/12], 
                None}},
             GridLines -> {Table[
                ArcCos[(d^2 + 75)/(20 d)], {d, 5, 15, 2}], {}}],
            ImageScaled[{.65, .3}]]
           }] &

enter image description here
POSTED BY: Kuba Podkalicki
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard