Hello, yes I have fixed it!

If you want to change the parameters n2 is the refractive index of the lens material and the initial ray height can be set by changing yint[1,1]

What I have left to do is create another loop that will add in more rays.

If you have any feedback/improvements on the code I would love to hear it as this is my first coding project since high school, and first with Mathematica.

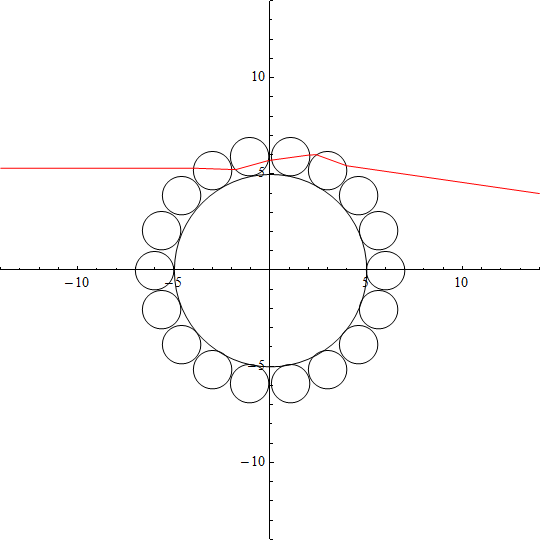
Here is what the code will output:

ClearAll["Global`*"]
(*draw circles*)
(*input data*)
LcircRad = 5;
ScircRad = 1;
n1 = 1; (*refractiv index of free space*)
n2 = 1.5; (*ref index of lens*)
(*angle per circle theta*)
theta = 2 ArcSin[ScircRad/(LcircRad + ScircRad)];
(*lenses per circle*)
nlens = Floor[2 \[Pi]/theta];
(*corrected angle per circle to ensure even distriubution*)
theta = N[2 \[Pi]/nlens];
(*populating arrays with x and y centres of small circles
ofset with \[Pi] so that first circle is drawn on the left*)
xcircle = 
  Table[(LcircRad + ScircRad) Cos[theta i + \[Pi]], {i, 0, nlens, 1}];
ycircle = 
  Table[(LcircRad + ScircRad) Sin[theta i + \[Pi]], {i, 0, nlens, 1}];
(*calculates number of rays*)
totalD = 2 (LcircRad + 
    2 ScircRad);(*total diameter of lens structure*)
raystarty = LcircRad + 2 ScircRad;(*starting height of first ray*)
raystartx = -3;(*starting x of rays*)
rayspacing = 1;(*vertical spacing between rays*)
nrays = Floor[totalD/rayspacing];
rayspacing = totalD/nrays;
(*populate the first intersection points & grad for ray plotting*)
(*
Do[yint[i,1]=raystarty-rayspacing(i-1),{i,1,nrays+1,1}]
Do[xint[i,1]=0,{i,1,nrays+1,1}]
Do[raygrad[i,1]=0,{i,1,nrays+1,1}]
*)

xint[1, 1] = -totalD;
yint[1, 1] = 5.3;
raygrad[1, 1] = 0;
j = 2;
xintemp = {1};
While[xintemp != {},

 y = raygrad [1, j - 1] (x - xint[1, j - 1]) + 
   yint[1, j - 
     1];(*y=m(x-x1)+y1 point grad form of straight line for ray at \
prev int point*)
 (*temp stores x int of line and circles and ingnores the solution \
which is the prev intersection using cases, rounded so that cases can \
remove the right thing*)
 xintemp =
  Select[
   Cases[
    Round[
     Flatten[Table[
       Select[
        NSolve[(x - xcircle[[i]])^2 + (y - ycircle[[i]])^2 == 
           ScircRad^2, x, WorkingPrecision -> 3][[All, 1, 2]],
        Element[#, Reals] &],
       {i, 1, nlens} ]],
     0.00001],
    Except[xint[1, j - 1]]]
   , # > xint[1, j - 1] &];
 (*solves the line for y using x intercepts*)
 yintemp = Round[
   Flatten[Table[
     Solve[
       ysol == raygrad [1, j - 1] (xintemp[[i]] - xint[1, j - 1]) + 
         yint[1, j - 1], ysol][[All, 1, 2]],
     {i, Dimensions[xintemp][[1]]}]]
   , 0.00001];
 (*find coord of new intersection closest to prev*)
 xint[1, j] = 
  Nearest[Table[{xintemp[[i]], yintemp[[i]]}, {i, 
      Dimensions[xintemp][[1]]}], {xint[1, j - 1], 
     yint[1, j - 1]}][[1, 1]];
 yint[1, j] = 
  Nearest[Table[{xintemp[[i]], yintemp[[i]]}, {i, 
      Dimensions[xintemp][[1]]}], {xint[1, j - 1], 
     yint[1, j - 1]}][[1, 2]];
 (*finds the circle number of the given intersection point*)
 circno = Position[
    Round[
     Table[
      Select[
       NSolve[(x - xcircle[[i]])^2 + (y - ycircle[[i]])^2 == 
          ScircRad^2, x][[All, 1, 2]],
       Element[#, Reals] &],
      {i, 1, nlens, 1} ],
     0.00001],
    xint[1, j]][[1, 1]];
 (*finds tangent and norm grad at point of intersection bw ray and \
circle*)
 normgrad = (ycircle[[circno]] - yint[1, j])/(
  xcircle[[circno]] - xint[1, j]);
 normang = ArcTan[normgrad];
 alpha1 = 
  ArcTan[Abs[(raygrad [1, j - 1] - normgrad)/(
    1 + raygrad [1, j - 1]*normgrad)]];
 alpha2 = ArcSin[(n1/n2) Sin[alpha1]];

 If[normang > 0, raygrad[1, j] = Tan[normang - alpha2], 
  raygrad[1, j] = Tan[normang + alpha2]];

 j = j + 1;]

(*
,{j,20}]
*)
(*after while loop is exited need to find intersection with ending \
line*)
y =.;
j = j - 1;
xint[1, j] = totalD;
yint[1, j] =
      raygrad [1, j - 1] (xint[1, j] - xint[1, j - 1]) + 
       yint[1, j - 1];
matrixer[functionName_Symbol] := 
 Normal[SparseArray[ReleaseHold[DownValues[#] /. # -> List]]] &[
  functionName]
(*turns xint and yint to matrix & removes the tailing entry which is \
bad cos of bad while loop
xintmatrix=matrixer[xint];
xintmatrix=Delete[xintmatrix,{1,Dimensions[xintmatrix][[2]]}];
yintmatrix=matrixer[yint];
yintmatrix=Delete[yintmatrix,{1,Dimensions[yintmatrix][[2]]}];*)
xintmatrix = matrixer[xint];
yintmatrix = matrixer[yint];
Show[Table[
  Graphics[Circle[{xcircle[[i]], ycircle[[i]]}, ScircRad]], {i, 1, 
   nlens, 1}], Graphics[Circle[{0, 0}, LcircRad]],
 Table[
  Graphics[{Red, 
    Line[{{xintmatrix[[1, o]], 
       yintmatrix[[1, o]]}, {xintmatrix[[1, o + 1]], 
       yintmatrix[[1, o + 1]]}}]}]
  , {o, Dimensions[xintmatrix][[2]] - 1}],
 PlotRange -> {{-1 totalD, 1 totalD}, {-1 totalD, 1 totalD}}, 
 Axes -> True]

It would be cool to see what this code does if this is a ray tracer. But when I run it - it did not work - error:

Coordinate { $CellContext`xint[1, 8], $CellContext`yint[1, 8]} should be a pair of numbers, or a Scaled or Offset form.

Do you have a fixed version?

Hi there, I am sure you are right.

I has something to do with the Do loops inside the loop I want to implement, when I un-comment out the Do loop all the loops inside it loose their colour formatting, you know how the variable you are incrementing has a different shade of blue, that goes away.

Can you please expand on your answer as I have no idea what you mean by initialisation. How does one correctly initialise?

EDIT: Just to be clear if you meant initialise as in set a value for it, i is the incrementing variable for that Do loop, as such it shouldn't have a value

Thanks