Hi guys,

I have code that I need to debug using workbench, I have some loop structures that I want to step through one increment at a time so I can trace through my code to see where it is going wrong. My code is a ray tracing simulation, it is really badly written and I haven't defined any functions for it, all the calculations are done on the fly in a notebook. From what I can tell from the Workbench documentation you can't debug a notebook, you have to debug functions that are written in a separate .m file. How can I go about debugging my notebook? I have tried copying and pasting it into an .m file but this doesn't seem to work.

If needed, here is the working code, it successfully traces rays through lenses:

ClearAll["Global`*"]
(*draw circles*)

(*input data*)
LcircRad = 5;
ScircRad = 1;
n1 = 1; (*refractiv index of free space*)
n2 = 1.4; (*ref index of lens*)

(*angle per circle theta*)
theta = 2 ArcSin[ScircRad/(LcircRad + ScircRad)];
(*lenses per circle*)
nlens = Floor[2 \[Pi]/theta];
(*corrected angle per circle to ensure even distriubution*)
theta = N[2 \[Pi]/nlens];

(*populating arrays with x and y centres of small circles
ofset with \[Pi] so that first circle is drawn on the left*)
xcircle = 
  Table[(LcircRad + ScircRad) Cos[theta i + \[Pi]], {i, 0, nlens, 1}];
ycircle = 
  Table[(LcircRad + ScircRad) Sin[theta i + \[Pi]], {i, 0, nlens, 1}];

(*calculates number of rays*)
totalD = 2 (LcircRad + 2 ScircRad);(*total diameter of lens structure*)


raystarty = LcircRad + 2 ScircRad;(*starting height of first ray*)
raystartx = -3;(*starting x of rays*)
rayspacing = 1;(*vertical spacing between rays*)
nrays = Floor[totalD/rayspacing];
rayspacing = 
  totalD/(nrays - 1);(*adjust ray spacing for even distriubution*)


(*populate the first intersection points & grad for ray plotting*)
Do[yint[i, 1] = raystarty, {i, nrays}]
Do[yint[i, 1] = raystarty - rayspacing (i - 1), {i, 2, nrays}]
Do[xint[i, 1] = -totalD, {i, 1, nrays + 1, 1}]
Do[raygrad[i, 1] = 0, {i, 1, nrays + 1, 1}]

Do[
 (*initialising variables for the while loop*)
 j = 2;
 xintemp = {1};

 While[xintemp != {},

    y = raygrad [k, j - 1] (x - xint[k, j - 1]) + yint[k, j - 1];(*y=
    m(x-x1)+y1 point grad form of straight line for ray at prev int \
point*)
    (*temp stores x int of line and circles and ingnores the solution \
which is the prev intersection using cases, 
    rounded so that cases can remove the right thing*)

    xintemp =
     Select[
      Cases[
       Round[
        Flatten[Table[
          Select[

           NSolve[(x - xcircle[[i]])^2 + (y - ycircle[[i]])^2 == 
              ScircRad^2, x, WorkingPrecision -> 3][[All, 1, 2]],
           Element[#, Reals] &],
          {i, 1, nlens} ]],
        0.00001],
       Except[xint[k, j - 1]]]
      , # > xint[k, j - 1] &];
    (*solves the line for y using x intercepts*)
    yintemp = Round[
      Flatten[Table[
        Solve[
          ysol == raygrad [k, j - 1] (xintemp[[i]] - xint[k, j - 1]) +
             yint[k, j - 1], ysol][[All, 1, 2]],
        {i, Dimensions[xintemp][[1]]}]]
      , 0.00001];
    (*find coord of new intersection closest to prev*)
    xint[k, j] = 
     Nearest[Table[{xintemp[[i]], yintemp[[i]]}, {i, 
         Dimensions[xintemp][[1]]}], {xint[k, j - 1], 
        yint[k, j - 1]}][[1, 1]];
    yint[k, j] = 
     Nearest[Table[{xintemp[[i]], yintemp[[i]]}, {i, 
         Dimensions[xintemp][[1]]}], {xint[k, j - 1], 
        yint[k, j - 1]}][[1, 2]];
    (*finds the circle number of the given intersection point*)
    circno = Position[
       Round[
        Table[
         Select[

          NSolve[(x - xcircle[[i]])^2 + (y - ycircle[[i]])^2 == 
             ScircRad^2, x][[All, 1, 2]],
          Element[#, Reals] &],
         {i, 1, nlens, 1} ],
        0.00001],
       xint[k, j]][[1, 1]];
    (*finds tangent and norm grad at point of intersection bw ray and \
circle*)
    normgrad = (ycircle[[circno]] - yint[k, j])/(
     xcircle[[circno]] - xint[k, j]);
    normang = ArcTan[normgrad];
    alpha1 = 
     ArcTan[Abs[(raygrad [k, j - 1] - normgrad)/(
       1 + raygrad [k, j - 1]*normgrad)]];
    alpha2 = ArcSin[(n1/n2) Sin[alpha1]];

    If[normang > 0, raygrad[k, j] = Tan[normang - alpha2], 
     raygrad[k, j] = Tan[normang + alpha2]];

    j = j + 1;
    jsave = j;]

   (*after while loop is exited, 
   this finds intersection with ending line*)
   xint[k, j - 1] = 
  totalD;(*this first one gets ingnored so needs to be repeated \
below, possible bug?*)
 xint[k, j - 1] = totalD;
 yint[k, j - 1] = 
  raygrad [k, j - 2]*(xint[k, j - 1] - xint[k, j - 2]) + 
   yint[k, j - 2];

 j = 2;
 , {k, nrays}]

matrixer[functionName_Symbol] := 
 Normal[SparseArray[ReleaseHold[DownValues[#] /. # -> List]]] &[
  functionName]

(*converts xint and yint into proper matrix so dimension can be found*)
xintmatrix = matrixer[xint];
yintmatrix = matrixer[yint];

Style[Show[
  Table[Graphics[Circle[{xcircle[[i]], ycircle[[i]]}, ScircRad]], {i, 
    1, nlens, 1}], Graphics[Circle[{0, 0}, LcircRad]],
  Table[
   Graphics[{Thin, Red, 
     Line[{{xint[k, o], yint[k, o]}, {xint[k, o + 1], 
        yint[k, o + 1]}}]}]
   , {k, nrays}, {o, Dimensions[xintmatrix][[2]] - 1}],
  PlotRange -> {{-.75 totalD, .75 totalD}, {-.5 totalD, .5 totalD}}, 
  Axes -> True], 
 AutoStyleOptions -> {"HighlightFormattingErrors" -> False}]

That produces something like this (except not red):

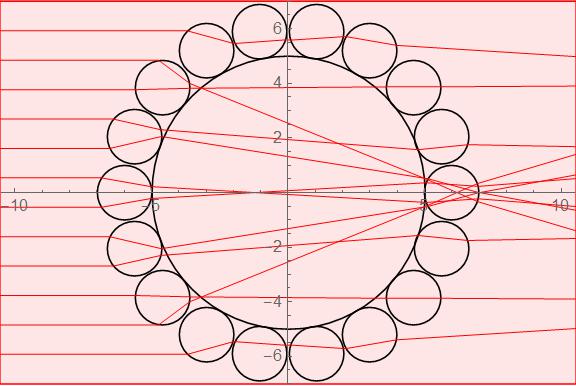
Then I am trying to add some code that makes the central circle act as an absorber. So if there is intersection with it the ray terminates. This is where I am having problems and I want to put this code into workbench to evaluate it step by step and track variables value as loops increment:

ClearAll["Global`*"]

(*draw circles*)
(*input data*)
LcircRad = 5;
ScircRad = 1;
n1 = 1;(*refractiv index of free space*)n2 = 1.65;(*ref index of \
lens*)(*angle per circle theta*)theta = 
 2 ArcSin[ScircRad/(LcircRad + ScircRad)];
(*lenses per circle*)
nlens = Floor[2 \[Pi]/theta];
(*corrected angle per circle to ensure even distriubution*)
theta = N[2 \[Pi]/nlens];

(*populating arrays with x and y centres of small circles ofset with \
\[Pi] so that first circle is drawn on the left*)
xcircle = 
  Table[(LcircRad + ScircRad) Cos[theta i + \[Pi]], {i, 0, nlens, 1}];
ycircle = 
  Table[(LcircRad + ScircRad) Sin[theta i + \[Pi]], {i, 0, nlens, 1}];

(*calculates number of rays*)
totalD = 2 (LcircRad + 
    2 ScircRad);(*total diameter of lens structure*)raystarty = 
 LcircRad + 
  2 ScircRad;(*starting height of first ray*)raystartx = \
-3;(*starting x of rays*)rayspacing = 1;(*vertical spacing between \
rays*)nrays = Floor[totalD/rayspacing];
rayspacing = 
 totalD/(nrays - 
    1);(*adjust ray spacing for even distriubution*)(*populate the \
first intersection points& grad for ray plotting*)Do[
 yint[i, 1] = raystarty, {i, nrays}]
Do[yint[i, 1] = raystarty - rayspacing (i - 1), {i, 2, nrays}]
Do[xint[i, 1] = -0.75 totalD, {i, 1, nrays + 1, 1}]
Do[raygrad[i, 1] = 0, {i, 1, nrays + 1, 1}]



Do[(*initialising variables for the while loop*)j = 2;
 xintemp = {1};
 bigint = 0;
 While[xintemp != {}, 
   y = raygrad[k, j - 1] (x - xint[k, j - 1]) + yint[k, j - 1];(*y=
   m(x-x1)+y1 point grad form of straight line for ray at prev int \
point*)(*temp stores x int of line and circles and ingnores the \
solution which is the prev intersection using cases,
   rounded so that cases can remove the right thing*)
   xintemp = 
    Select[Cases[
      Round[Flatten[
        Table[Select[
          NSolve[(x - xcircle[[i]])^2 + (y - ycircle[[i]])^2 == 
             ScircRad^2, x, WorkingPrecision -> 3][[All, 1, 2]], 
          Element[#, Reals] &], {i, 1, nlens}]], 0.00001], 
      Except[xint[k, j - 1]]], # > xint[k, j - 1] &];
   (*solves the line for y using x intercepts*)
   yintemp = 
    Round[Flatten[
      Table[Solve[
         ysol == raygrad[k, j - 1] (xintemp[[i]] - xint[k, j - 1]) + 
           yint[k, j - 1], ysol][[All, 1, 2]], {i, 
        Dimensions[xintemp][[1]]}]], 0.00001];
   (*find coord of new intersection closest to prev*)
   xint[k, j] = 
    Nearest[Table[{xintemp[[i]], yintemp[[i]]}, {i, 
        Dimensions[xintemp][[1]]}], {xint[k, j - 1], 
       yint[k, j - 1]}][[1, 1]];
   yint[k, j] = 
    Nearest[Table[{xintemp[[i]], yintemp[[i]]}, {i, 
        Dimensions[xintemp][[1]]}], {xint[k, j - 1], 
       yint[k, j - 1]}][[1, 2]];
   (*finds the circle number of the given intersection point*)
   circno = 
    Position[
      Round[Table[
        Select[NSolve[(x - xcircle[[i]])^2 + (y - ycircle[[i]])^2 == 
            ScircRad^2, x][[All, 1, 2]], Element[#, Reals] &], {i, 1, 
         nlens, 1}], 0.00001], xint[k, j]][[1, 1]];
   (*finds tangent and norm grad at point of intersection bw ray and \
circle*)normgrad = (ycircle[[circno]] - 
       yint[k, j])/(xcircle[[circno]] - xint[k, j]);
   normang = ArcTan[normgrad];
   alpha1 = 
    ArcTan[Abs[(raygrad[k, j - 1] - normgrad)/(1 + 
         raygrad[k, j - 1]*normgrad)]];
   alpha2 = ArcSin[(n1/n2) Sin[alpha1]];
   If[normang > 0, raygrad[k, j] = Tan[normang - alpha2], 
    raygrad[k, j] = Tan[normang + alpha2]];

   (*test for intersection with big circle,
   and if that intersection is closer to the prev intersection then \
the loop is exited*)
   y = raygrad[k, j - 1] (x - xint[k, j]) + yint[k, j];
   xbigintemp = 
    NSolve[x^2 + y^2 == LcircRad^2, x, WorkingPrecision -> 3][[All, 1,
       2]];
   ybigintemp = 
    raygrad[k, j - 1] (xbigintemp - xint[k, j]) + yint[k, j];
   xbigint = 
    Nearest[{{xbigintemp[[1]], ybigintemp[[1]]}, {xbigintemp[[2]], 
          ybigintemp[[2]]}}, {xint[k, j - 1], yint[k, j - 1]}][[1, 
        1]] ybigint = 
     Nearest[{{xbigintemp[[1]], ybigintemp[[1]]}, {xbigintemp[[2]], 
           ybigintemp[[2]]}}, {xint[k, j - 1], yint[k, j - 1]}][[1, 
         2]] If[EuclideanDistance[{xint[k, j], 
           yint[k, j]}, {xint[k, j - 1], yint[k, j - 1]}] > 
         EuclideanDistance[{xbigint, ybigint}, {xint[k, j - 1], 
           yint[k, j - 1]}], xint[k, j] = xbigint;
        yint[k, j] = ybigint; xintemp = {}; bigint = 1] j = j + 1;

   ](*while end*) 

  If[bigint != 1,(*after while loop is exited,
   this finds intersection with ending line*)
   xint[k, j - 1] = 0.75 totalD;
   yint[k, j - 1] = 
    raygrad[k, j - 2]*(xint[k, j - 1] - xint[k, j - 2]) + 
     yint[k, j - 2]];, {k, nrays}]

matrixer[functionName_Symbol] := 
 Normal[SparseArray[ReleaseHold[DownValues[#] /. # -> List]]] &[
  functionName]

(*converts xint and yint into proper matrix so dimension can be found*)


xintmatrix = matrixer[xint];
yintmatrix = matrixer[yint];

Style[Show[
  Table[Graphics[Circle[{xcircle[[i]], ycircle[[i]]}, ScircRad]], {i, 
    1, nlens, 1}], Graphics[Circle[{0, 0}, LcircRad]], 
  Table[Graphics[{Thin, Red, 
     Line[{{xint[k, o], yint[k, o]}, {xint[k, o + 1], 
        yint[k, o + 1]}}]}], {k, nrays}, {o, 
    Dimensions[xintmatrix][[2]] - 1}],(*PlotRange\[Rule]{{-1totalD,
  1totalD},{-1totalD,1totalD}},*)Axes -> True], 
 AutoStyleOptions -> {"HighlightFormattingErrors" -> False}]