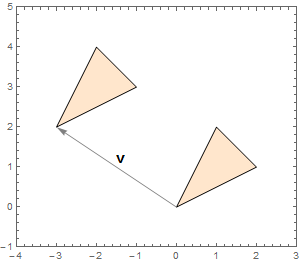
Sounds like a homework assignment. I love these because I always learn so much. Let's try using the Mathematica 10 Geometry routines.

triangle = Triangle[{{0, 0}, {2, 1}, {1, 2}}];
triangleTransformed = 
 TransformedRegion[triangle, TranslationTransform[{-3, 2}]]

Triangle[{{-3, 2}, {-1, 3}, {-2, 4}}]

I always like to linger over the graphic.

Graphics[
 {EdgeForm[Black], FaceForm[LightOrange],
  triangle, triangleTransformed,
  Gray,
  Arrow[{{0, 0}, {-3, 2}}],
  Text[Style["v", Black, 14, Bold, 
    FontFamily -> "Helvetica"], {-3, 2}/2, {-1, -1}]
  },
 PlotRangePadding -> 1,
 Frame -> True,
 ImageSize -> 300]

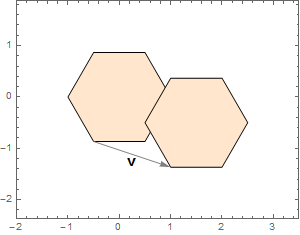
The polygon points look like a hexagon and we can easily construct that from a Table. You could use N on the expression to see the points are essentially the same as given in the problem. I just didn't feel like copying them all in.

polygon = 
 Polygon[Table[{Cos[t Degree], Sin[t Degree]}, {t, 0, 360 - 60, 60}]]
polygonTransformed = 
 TransformedRegion[polygon, TranslationTransform[{1.5, -0.5}]]

Polygon[{{1, 0}, {1/2, Sqrt[3]/2}, {-(1/2), Sqrt[3]/2}, {-1, 0}, {-(1/2), -(Sqrt[3]/2)}, {1/2, -(Sqrt[3]/2)}}]
Polygon[{{2.5, -0.5}, {2., 0.366025}, {1., 0.366025}, {0.5, -0.5}, {1., -1.36603}, {2., -1.36603}}]

The plotting is essentially the same.

Graphics[
 {EdgeForm[Black], FaceForm[LightOrange],
  polygon, polygonTransformed,
  Gray,
  Arrow[{{-(1/2), -(Sqrt[3]/
      2)}, {-(1/2), -(Sqrt[3]/2)} + {1.5, -0.5}}],
  Text[Style["v", Black, 14, Bold, 
    FontFamily -> "Helvetica"], {-(1/2), -(Sqrt[3]/2)} + {1.5, -0.5}/
     2, {0, 1}]
  },
 PlotRangePadding -> 1,
 Frame -> True,
 ImageSize -> 300]