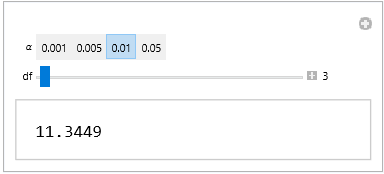
I get the appropriate values:
df = 3;
alpha = 0.01;
InverseCDF[ChiSquareDistribution[df], 1 - alpha]
(* 11.34486673014437` *)
alpha = 0.05;
InverseCDF[ChiSquareDistribution[df], 1 - alpha]
(* 7.814727903251181` *)
Also, there are many, many ways to mimic the calculator you reference. Here's one way:
Manipulate[
InverseCDF[ChiSquareDistribution[df], 1 - \[Alpha]],
{{\[Alpha], 3}, {0.001, 0.005, 0.01, 0.05}},
{{df, 1}, 1, 120, 1, Appearance -> "Labeled"}]