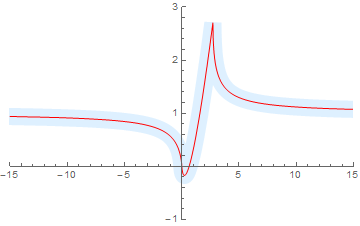
Mathematica definitely gives the same values (where I've plotted the real part of the inverse using the two definitions):
f[x_] := x/Log[x];
fInverse = InverseFunction[f];
Plot[{Re[fInverse[x]], Re[-x ProductLog[-1/x]]}, {x, -15, 15},
PlotStyle -> {{Thickness[0.05], LightBlue}, {Thin, Red}},
PlotRange -> {{-15, 15}, {-1, 3}}]
with output
In Wolfram Alpha where is it that you see the wrong plot? The link you show displays the real part and the imaginary part of the inverse and not the original function and its inverse.