Hi, I am trying to plot a streamfunction which is given in spherical coordinates
phis = 1/r*(1 - Sin[\[Theta]]^2*(2*Sin[a]^2 - Sin[\[Theta]]^2)/Sin[a]^4);
I find that I get a different answer depending on whether I a) convert the streamfunction itself to cartesian coordinates (either manually or using TransformCoordinates) and then use Ux=dphis/dy and Uy=-dphis/dx or b) calculate the components of the stream function in the r, theta direction(Ur=1/(r^2Sin[[Theta]]))d(phis)/dt, Ut=-1/(rSin[[Theta]])d(phis)/dr) and then convert to cartesian coordinates.
In the former case, the orientation of the vortices is correct but they are asymmetric where they should be symmetric. In the second case, the vortices are symmetric but they are rotated -90 degrees.
The code I am using for case A is
a = 5*Pi/180;
phis = 1/r*(1 -
Sin[\[Theta]]^2*(2*Sin[a]^2 - Sin[\[Theta]]^2)/Sin[a]^4);
phic = TransformedField["Spherical" -> "Cartesian",
phis, {r, \[Theta], \[CurlyPhi]} -> {x, y, z}];
u = D[phic2, z];
v = -D[phic2, y];
field = {u, v};
StreamDensityPlot[
field /. x -> 0 // Evaluate, {y, -10, 10}, {z, -10, 10},
ColorFunction -> (ColorData["Rainbow"][Rescale[#5, {0, 100}]] &),
ColorFunctionScaling -> False, StreamPoints -> Fine,
StreamStyle -> Black]
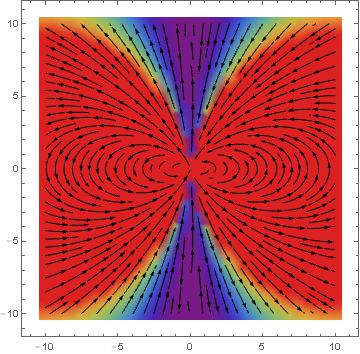
Note that I get the same result if
u = D[phic, z];
v = -D[phic, y];
The code I am using for Case B is
dphisdr = -((
1 - Csc[\[Pi]/
36]^4 Sin[\[Theta]]^2 (2 Sin[\[Pi]/36]^2 - Sin[\[Theta]]^2))/r^2)
dphisdt = (
2 Cos[\[Theta]] Csc[\[Pi]/36]^4 Sin[\[Theta]]^3 -
2 Cos[\[Theta]] Csc[\[Pi]/
36]^4 Sin[\[Theta]] (2 Sin[\[Pi]/36]^2 - Sin[\[Theta]]^2))/r
field = {(1/(r^2*Sin[\[Theta]]))*dphisdt, -1/(r*Sin[\[Theta]])*
dphisdr};
transfield =
TransformedField["Polar" -> "Cartesian",
field, {r, \[Theta]} -> {x, y}];
StreamDensityPlot[transfield, {x, -10, 10}, {y, -10, 10},
ColorFunction -> (ColorData["Rainbow"][Rescale[#5, {0, 100}]] &),
ColorFunctionScaling -> False, StreamPoints -> Fine,
StreamStyle -> Black]
And the resultant image is 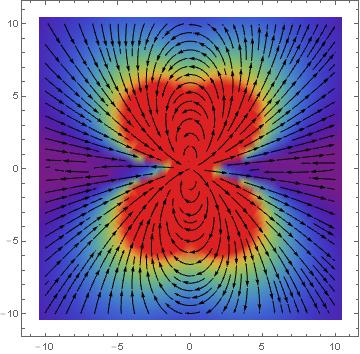
I assume the issue involves my use of the "TransformedCoordinates" function but I am not sure how to work around it?