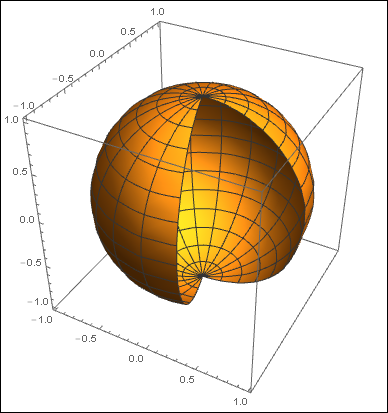
Just to be clear, since there are more than one convention:
In SphericalPlot3D the first angle argument is the "latitudinal" angle. And the second angle argument is the "longitudinal" angle.
In the SphericalPlot3D case, the Mathematica documentation does not follow the most common uses of the greek letters theta and phi.
f[\[Theta]_, \[Phi]_] := Module[
{a, b, c, d},
a = ((3.14*.005) (1.887 - 1.792))/
((.000522)*Cos[-.7454*Sin[\[Theta]]*Cos[\[Phi]] + .6626*Cos[\[Theta]]]);
b = (1 - Cos[.7454*Sin[\[Theta]]*Cos[\[Phi]] + .6626*Cos[\[Theta]]]^2)*
(1 -Cos[-.7454*Sin[\[Theta]]*Cos[\[Phi]] + .6626*Cos[\[Theta]]])^2;
c = a*b;
d = (Cos[c])^2
]
SphericalPlot3D[f[polar, azimuthal], {polar, 0, \[Pi]}, {azimuthal, 0, 5}]