Hi Camilo,
So, it looks like the numbers are the directions to move. But if you are going for a graphic, all you really need is a position in the matrix.
Instead of using 0 for the entries that don't count, I used 0.0 so that I can distinguish the position of the newly generated move by looking for an Integer.
Then I generated a graphic of each of the moves by drawing a line from each move to the next.
I'm not very advanced, functional programming-wise, so I used a Do loop.
Meander[n_, t_] :=
Module[{RND, walk, VonNeumann, initConf},
RND := Random[Integer, {1, 4}];
initConf =
ReplacePart[Table[0.0, {2 n + 1}, {2 n + 1}], RND, {n + 1, n + 1}];
walk[1, 0.0, 0.0, 0.0, 0.0] := 0.0;
walk[2, 0.0, 0.0, 0.0, 0.0] := 0.0;
walk[3, 0.0, 0.0, 0.0, 0.0] := 0.0;
walk[4, 0.0, 0.0, 0.0, 0.0] := 0.0;
walk[0.0, 3, 0.0, 0.0, 0.0] := RND;
walk[0.0, 0.0, 4, 0.0, 0.0] := RND;
walk[0.0, 0.0, 0.0, 1, 0.0] := RND;
walk[0.0, 0.0, 0.0, 0.0, 2] := RND;
walk[0.0, 1, 0.0, 0.0, 0.0] := 0.0;
walk[0.0, 2, 0.0, 0.0, 0.0] := 0.0;
walk[0.0, 4, 0.0, 0.0, 0.0] := 0.0;
walk[0.0, 0.0, 1, 0.0, 0.0] := 0.0;
walk[0.0, 0.0, 2, 0.0, 0.0] := 0.0;
walk[0.0, 0.0, 3, 0.0, 0.0] := 0.0;
walk[0.0, 0.0, 0.0, 2, 0.0] := 0.0;
walk[0.0, 0.0, 0.0, 3, 0.0] := 0.0;
walk[0.0, 0.0, 0.0, 4, 0.0] := 0.0;
walk[0.0, 0.0, 0.0, 0.0, 1] := 0.0;
walk[0.0, 0.0, 0.0, 0.0, 3] := 0.0;
walk[0.0, 0.0, 0.0, 0.0, 4] := 0.0;
walk[0.0, 0.0, 0.0, 0.0, 0.0] := 0.0;
VonNeumann[func_, lat_] :=
MapThread[func,
Map[RotateRight[lat, #] &, {{0.0, 0.0}, {1, 0.0}, {0.0, -1}, {-1,
0.0}, {0.0, 1}}], 2];
NestList[VonNeumann[walk, #] &, initConf, t]]
out = Meander[6, 126]; bb = {}; Do[
AppendTo[bb, Position[out[[d, All]], _Integer]], {d, 1,
127}]; Graphics[Line[Flatten[bb, 1]]]
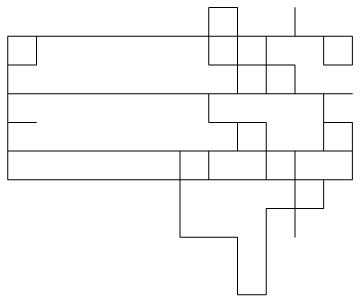
It looks as though your random walk is actually on a torus connected left-to-right and top-to-bottom. That would be interesting to draw!
Eric