Yes, Michael Rogers, that is what I did. I cannot find the function for integrate the InterpolatingFunction, so I just copy the command give by the "Automatic Options". I'm able to find the area under the graph of the InterpolatingFunction, but unable to choose specific method or rule. My predecessor used the Simpson's Rule for the rules of definite integrals. So, now I need to know which rule that Mathematica choose from the rules of definite integrals (there's quiet a few, searched in Wikipedia).

I apologize if I misunderstand some points.

The first integration will be the of the piecewise polynomial equation. Then produces InterpolatingFunction, which is also a symbolic function. I am able to obtain the numerical value with the options given, from the option "Evaluate at point 3"

Then the InterpolatingFunction is an order-4 InterpolatingFunction?, the integration will be an order-5?

The Integration of the InterpolatingFunction is use to find the area under the graph for the InterpolatingFunction, which was similar to Simpson's Rule or Riemann Integral or others.

Or do you mean "Integrate integrates the polynomials symbolically and evaluates them at the endpoints of their subintervals; ", it follows the 4th Order RungeKutta Method and the subintervals is also 1/100?

Sorry if I seems to behave not professional with all these questions.

Thank you Michael Rogers, this have given me an idea of how the integration works.

It's just that, for integrations without using Mathematica, we would use Simpson's Rules or Trapeziodal rule for integration for numerical integration, to obtain the value for the initial value before it. But in Mathematica without numerical integration, the InterpolatingFunction only show a graph or a plot (without any polynomials shown). Well I did obtain an accurate value for the integration of the InterpolatingFunction.

There's the set of rules in Mathematica for integration. So, now I need to know which is the correct integration rule that is default for Mathematica.

tutorial/NIntegrateIntegrationRules

I believe Mathematica automatic chooses the rule for the Integration, so what command do I need to type to find out which method it used?

Sorry for the confusion, here's what I did. I NDSolve the equation with 4th Order RungeKutta Method

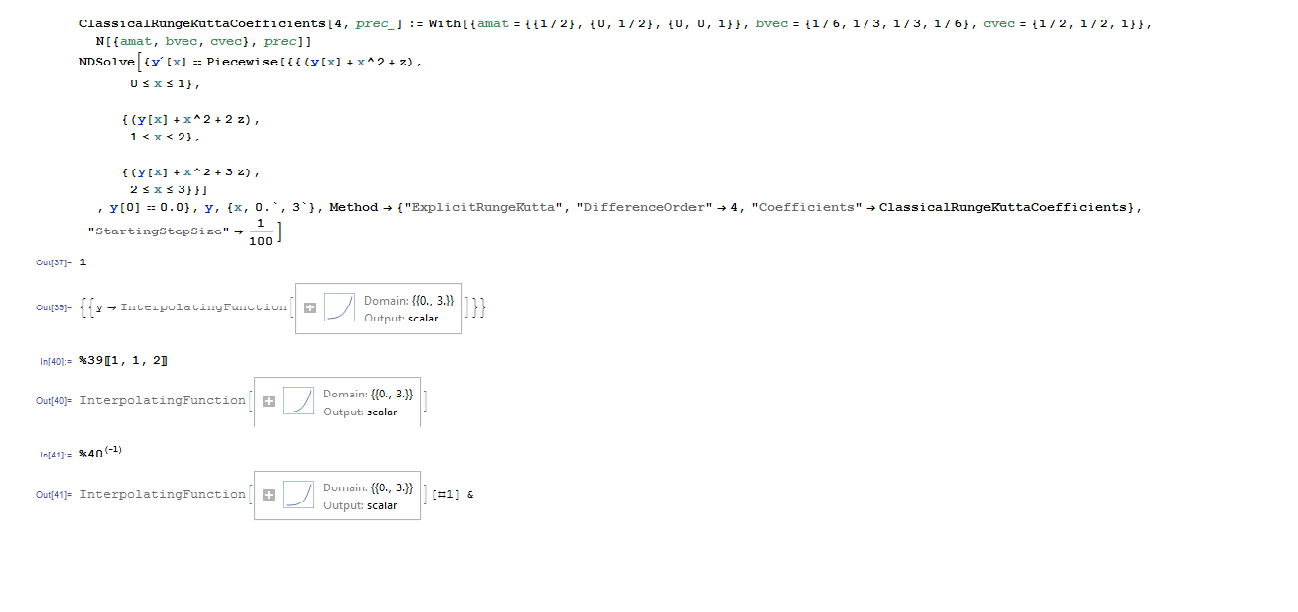
 In[37]:= z = 1
    ClassicalRungeKuttaCoefficients[4, prec_] := 
     With[{amat = {{1/2}, {0, 1/2}, {0, 0, 1}}, 
       bvec = {1/6, 1/3, 1/3, 1/6}, cvec = {1/2, 1/2, 1}}, 
      N[{amat, bvec, cvec}, prec]]
    NDSolve[{Derivative[1][y][x] == Piecewise[{{(y[x] + x^2 + z),
          0 <= x <= 1},

     {(y[x] + x^2 + 2 z),
      1 <= x <= 2},

     {(y[x] + x^2 + 3 z),
      2 <= x <= 3}}]
  , y[0] == 0.0}, y, {x, 0.`, 3`}, 
 Method -> {"ExplicitRungeKutta", "DifferenceOrder" -> 4, 
   "Coefficients" -> ClassicalRungeKuttaCoefficients}, 
 "StartingStepSize" -> 1/100]

Out[37]= 1

Out[39]= {{y -> InterpolatingFunction[{{0., 3.}}, <>]}}

Then I chose the option "Get Solution"

In[40]:= %39[[1, 1, 2]]

Out[40]= InterpolatingFunction[{{0., 3.}}, <>]

After that, there's another option, "Integrate", that's where the new integration result show up. The thing is, the code in the notebook and posted here is different. I would like to know does this new integration chose the previous integration method done, the 4th Order RungeKutta Method? or Mathematica chose another method?

In[41]:= 
\!\(\*SuperscriptBox[\(%40\), 
TagBox[
RowBox[{"(", 
RowBox[{"-", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)

Out[41]= InterpolatingFunction[{{0., 3.}}, <>][#1] &

Here's what I have done,

1) I try used f = NDSolve specified using RungeKutta 4th Order Method. 2) There's an option that have option to integrate "f" for me and I just chose the option to integrate again.

\!\(\*SuperscriptBox[\(f[\([\)\(1, 1, 2\)\(]\)]\), 
TagBox[
RowBox[{"(", 
RowBox[{"-", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[1]

Then I obtain the answer for "f" integrated another time.

So, what is the automatic default rule for this integration? From the manual, there's "Trapezoidal Rule", "Multipanel Rule" and so on. How do I know which rule that Mathematica chose?