Therefore my question: Why does the substitution of f with the command
"where" sometimes work and with a small variation it does not work
anymore.
it's all about input interpretation, of course: The program (Mathematica) has a free language input (the orange equal sign), working with it one gets
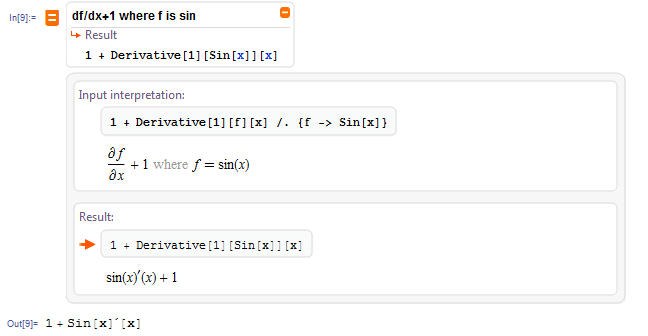
as you see, the input interpretation is correct in
$\LaTeX$, but not in Mathematica, it must be
In[18]:= 1 + Derivative[1][f][x] /. {f -> Sin}
Out[18]= 1 + Cos[x]
Two other interpretations missing the point are
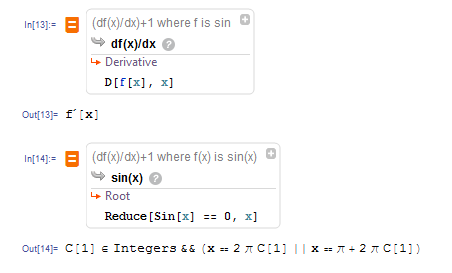
to be honest I was inapt to get the result out of the free language input with Mathematica 10.1 within half an hour.