I would also be grateful for responses to this from those with experience using Mathematica for control theory. In the code below, I treat the transfer function as that of the complete system. (Not a component with feedback around it.)
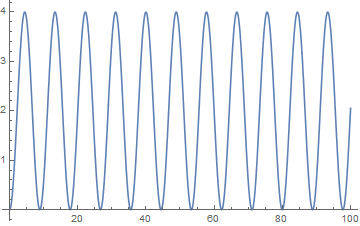
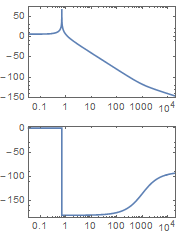
I observe that the transfer function is unstable, with conjugate poles on the axis. The OutputResponse to a step is oscillatory. I don't think a Bode plot of such a system is meaningful.
syss = (1 + 0.001 s)/(s^2 + 0.5);
sys = TransferFunctionModel[{{syss}}, s];
BodePlot[sys, FeedbackType -> None, PhaseRange -> {-Pi, Pi}]
In[4]:= (* poles on the axis == unstable *)
TransferFunctionPoles[sys]
Out[4]= {{{0. - 0.707107 I, 0. + 0.707107 I}}}
In[5]:= sysOutput = OutputResponse[sys, UnitStep[t], t] // Chop
Out[5]= {2. (-1. Cos[0.707107 t] UnitStep[t] +
1. Cos[0.707107 t]^2 UnitStep[t] +
0.000707107 Sin[0.707107 t] UnitStep[t] +
1. Sin[0.707107 t]^2 UnitStep[t])}
In[6]:= Plot[sysOutput, {t, 0, 100}]