And here is a numerical solution for your nonlinear system, with made up parameter values. When forming systemB, I used Thread so equations would be formatted individually, so they could be joined with the initial conditions. I also attach the notebook.
In[1]:= B = {{(p0 - q0)*(v0/(1 + \[Beta]0 ((x2[t])^2))) - d0, 0,
0}, {(1 - p0 +
q0)*(v0/(1 + \[Beta]0 ((x2[t])^2))), (p1 -
q1)*(v1/(1 + \[Beta]1 ((x2[t])^2))) - d1,
0}, {0, (1 - p1 + q1)*(v1/(1 + \[Beta]1 ((x2[t])^2))), -d2}}
Out[1]= {{-d0 + ((p0 - q0) v0)/(1 + \[Beta]0 x2[t]^2), 0,
0}, {((1 - p0 + q0) v0)/(
1 + \[Beta]0 x2[t]^2), -d1 + ((p1 - q1) v1)/(1 + \[Beta]1 x2[t]^2),
0}, {0, ((1 - p1 + q1) v1)/(1 + \[Beta]1 x2[t]^2), -d2}}
In[2]:= initB = {x0[0] == x00, x1[0] == x10, x2[0] == x20};
In[12]:= X[t_] = {x0[t], x1[t], x2[t]};
In[13]:= systemB = Thread[X'[t] == B.X[t]];
In[14]:= equations = Join[systemB, initB];
In[7]:= par = {q0 -> .5, q1 -> .5, v0 -> 1, v1 -> 1, x00 -> 100,
x10 -> 0, x20 -> 0, p0 -> .5, p1 -> .4, p2 -> .5, d0 -> .2,
d1 -> .3, d2 -> .4, \[Beta]0 -> 1, \[Beta]1 -> 1};
In[8]:= equations /. par
Out[8]= {Derivative[1][x0][t] == -0.2 x0[t],
Derivative[1][x1][t] == (1. x0[t])/(1 + x2[t]^2) +
x1[t] (-0.3 - 0.1/(1 + x2[t]^2)),
Derivative[1][x2][t] == -0.4 x2[t] + (1.1 x1[t])/(1 + x2[t]^2),
x0[0] == 100, x1[0] == 0, x2[0] == 0}
In[15]:= {fx0, fx1, fx2} =
NDSolveValue[equations /. par, {x0, x1, x2}, {t, 0, 100}];
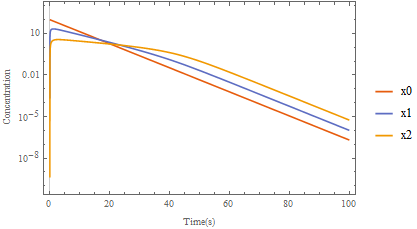
In[17]:= LogPlot[{fx0[t], fx1[t], fx2[t]}, {t, 0, 100},
PlotLegends -> {"x0", "x1", "x2"}, PlotTheme -> "Scientific",
FrameLabel -> {"Time(s)", "Concentration"}]
 Attachments:
Attachments: