Hi Giuseppe,
... so I decided to write an algorithm by myself.
Excellent idea!
As a start you could have written at least the definition of the lines in WL ... Well, anyway, here my solution, it is pretty straightforward:
ClearAll["Global`*"]
p = {p1, p2, p3};
g = {g1, g2, g3}/Sqrt[g1^2 + g2^2 + g3^2];
(* function to calculate distance between line and point: *)
lineDist[line : {g1_, g2_, g3_}, point : {p1_, p2_, p3_}] =
FullSimplify[Norm[p\[Cross]g], Thread[{p1, p2, p3, g1, g2, g3} \[Element] Reals]];
(* your four lines *)
v = {{{77.007, 32.46, 177.79}, {139.398, -309.133, -116.29}},
{{-79.504, 31.969, -179.158}, {31.886, -367.752, 99.796}},
{{-77.401, 32.855, 174.843}, {25.944, -350.134, -129.523}},
{{80.781, 32.154, -176.942}, {-149.572, -326.383, 84.57}}};
(* search for the point, where the max-distance is minimized *)
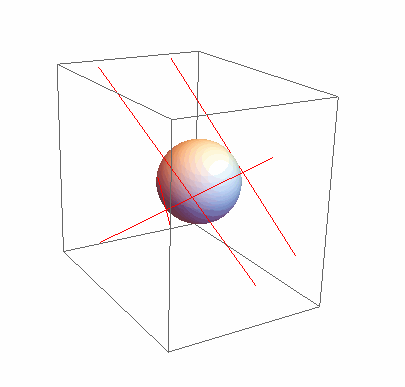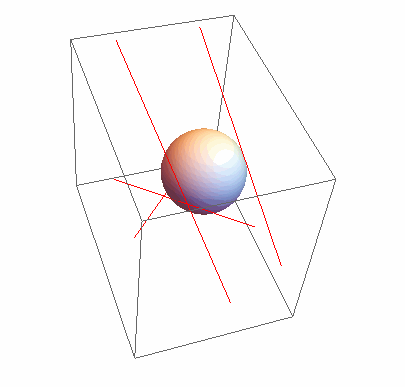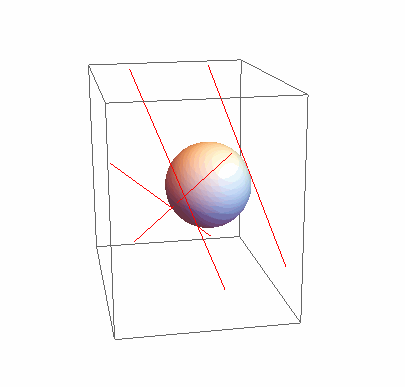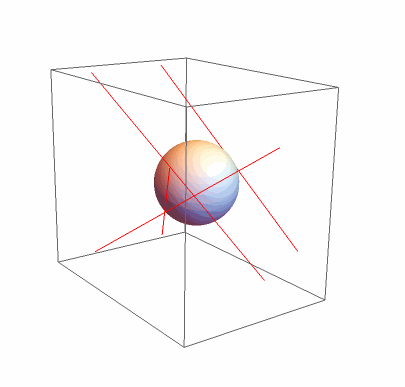
sol = Minimize[Max[lineDist[#1, p - #2] & @@@ ({#2 - #1, #1} & @@@ v)], p]
Graphics3D[{{Red, Line[v]}, Sphere[p /. sol[[2]], sol[[1]]]}, SphericalRegion -> True]
The result is:
Regards Henrik