Hi, I am facing troubles to solve the following 2nd order ordinary differential equation

{x'[t] == v[t],  v'[t] == 0.4 Sign[v[t]] UnitBox[v[t], x[t]] - 0.1 v[t] - x[t]}

Apparently, this is a nonlinear ODE, moreover, it contains a discontinuity (step) in both variables. I solve it numerically using

sol = NDSolve[{x'[t] == v[t], v'[t] == 0.4 Sign[v[t]] UnitBox[v[t], x[t]] - 0.1 v[t] - x[t], x[0] == 1., v[0] == 1.}, 
{v[t], x[t]}, {t, 0, 30}]

Plotting the solution using

ParametricPlot[Evaluate[{x[t], v[t]} /. sol], {t, 0, 30}]

I get

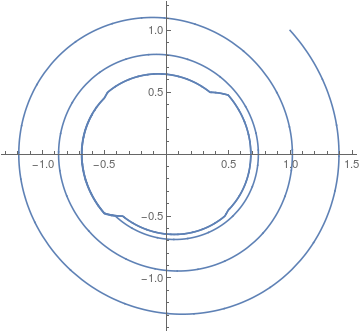
This suggests that there is a limit cycle. Indeed, this is confirmed by plotting the phase portrait by

f2 = StreamPlot[{v, 0.4` Sign[v] UnitBox[v, x] - 0.1` v - x}, {x, -2, 2}, {v, -2, 2}, StreamStyle -> LightGray];

and plotting it together with the previous solution

Show[f1, f2]

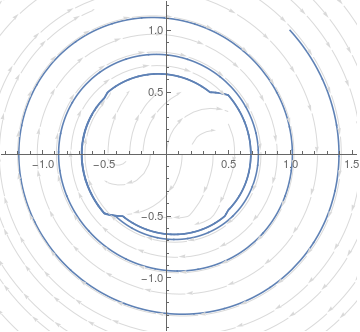
But now, if I set the initial conditions to inside the orbit, the solution fails

sol = NDSolve[{x'[t] == v[t], v'[t] == 0.4 Sign[v[t]] UnitBox[v[t], x[t]] - 0.1 v[t] - x[t], x[0] == 0.1., v[0] == 0.1.}, 
    {v[t], x[t]}, {t, 0, 30}]

f3 = ParametricPlot[Evaluate[{x[t], v[t]} /. sol], {t, 0, 4.1}, PlotStyle -> Red]

Show[f1, f2, f3]`

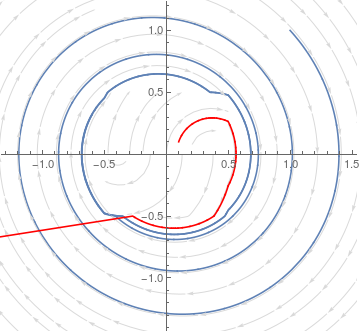
What can be done about it? I tried changing the solver and it did not help. I tried to insert the WhenEvent together with CrossDiscontinuity option. No way.