Read CellularAutomaton about the configurations developed so far.
The book A New Kind of Science is full of computational machinery (tag systems, cellular automata, Turing machines, ...).
See current post CellularAutomaton Code Jam Wolfram Summer School 2015 about function driven CA.
As far as representation is concerned, it is easy to display a CA onto a disk
Clear[circularCA]
circularCA[r_Integer, s_Integer] :=
Block[{c = CellularAutomaton[r, {{1}, 0}, {s, All}]},
Graphics[
Flatten[Table[{If[c[[o, oo]] == 1, Black, White],
Disk[{0, 0},
o, {Pi - (oo - (s + 1 - (o - 1))) (2 Pi)/(2 o - 1),
Pi - ((oo + 1) - (s + 1 - (o - 1))) (2 Pi)/(2 o - 1)}]}, {o,
s + 1, 1, -1}, {oo, s + 1 - (o - 1), s + 1 + (o - 1)}], 1],
PlotLabel ->
"Rule " <> ToString[r] <> " using " <> ToString[s] <> " steps",
Frame -> True]
] /; 1 <= r <= 256 && s > 0
giving
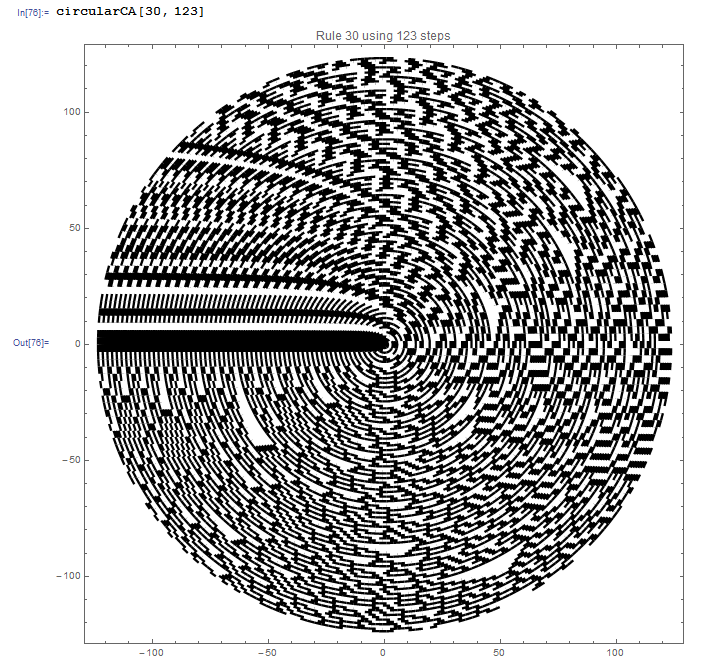
This circular form could raise the question whether the CA is stable against back-development (starting with the outer circular ring inwards and again outwards from the center ad inf.): Once you have it you ignore of course the
$\pi$ branch from the first run outwards.
You can also fill a matrix in different ways with a CA output (setting the starting point to [[1,1]]), getting pictures like this
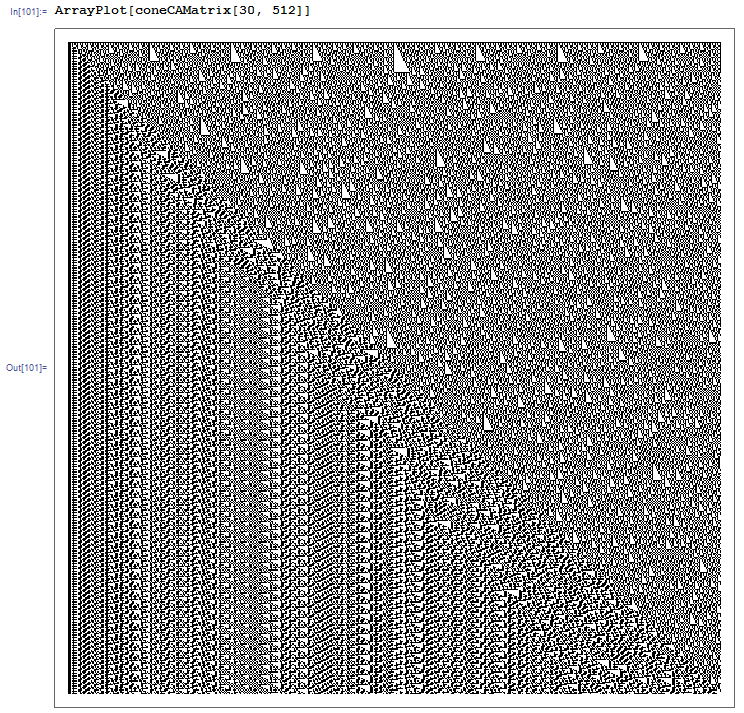
once they are in natural matrix form, one can do matrix operations with them

all this is very old (2009).