Example data.
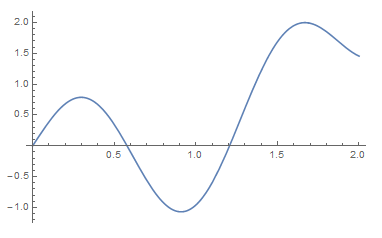
data1 = Table[{x, Sin[5 x] + x^2 - x}, {x, 0, 2, 0.1}]
(*{{0., 0.}, {0.1, 0.389426}, {0.2, 0.681471}, {0.3, 0.787495}, {0.4,
0.669297}, {0.5,
0.348472}, {0.6, -0.09888}, {0.7, -0.560783}, {0.8, -0.916802}, \
{0.9, -1.06753}, {1., -0.958924}, {1.1, -0.59554}, {1.2, -0.0394155}, \
{1.3, 0.60512}, {1.4, 1.21699}, {1.5, 1.688}, {1.6, 1.94936}, {1.7,
1.98849}, {1.8, 1.85212}, {1.9, 1.63485}, {2., 1.45598}}*)
Then Integrate data1
SS = Integrate[Interpolation[data1, InterpolationOrder -> 8][x], x];
m = 0.1; Sol = Table[{x, SS}, {x, 0, 2, m}]
(*{{0., 0.}, {0.1, 0.0198172}, {0.2, 0.0746065}, {0.3, 0.149853}, {0.4,
0.224563}, {0.5, 0.276896}, {0.6, 0.289999}, {0.7, 0.256625}, {0.8,
0.181395}, {0.9,
0.0801592}, {1., -0.023399}, {1.1, -0.103067}, {1.2, -0.136034}, \
{1.3, -0.107984}, {1.4, -0.0161135}, {1.5, 0.130673}, {1.6,
0.314434}, {1.7, 0.513069}, {1.8, 0.706226}, {1.9, 0.880768}, {2.,
1.03448}}*)
You can change "m" and "InterpolationOrder".
Check:
{NIntegrate[Sin[5 x] + x^2 - x, {x, 0, 2}],
NIntegrate[Interpolation[data1, InterpolationOrder -> 8][x], {x, 0, 2}]}
(*{1.03448, 1.03448}*)