Press et al in Numerical Recipes in C recommend Romberg Integration, which uses Neville's algorithm, a form of polynomial interpolation. Whether or not that gives the same result as integrating an interpolating function is not known to me.

The code implements a riemann sum and can be approximated by a 0 order Interpolation in your code.

You can get the upper riemann sum by using:

Rest[data[[All, 2]]].Differences[data[[All, 1]]]

Integration is an operation applied to functions, not data points. That's why various approximations were suggested.

There are proper numerical methods for integrating data points. You don't begin by arbitrarily approximating the function and then integrating it.

In general, you don't do an interpolation of the data and then symbolically integrate it. The basic ones are not obscure. The basic ones (Upper and Lower Riemann, trapizoid rule, Simpsons rule) are highschool AP Calculus Topics.

In the case above, a linear interpolation correspondes to the trapezoid rule. Still, it is preferable to use the trapezoid rule directly rather than using a linear interpolation. Even if they are symbolically the same, with floating point numbers, they may not be.

Sean,

could you expand; I'm looking for a result like

   Nintegrate[data1] = {{x1, y1?},{x2, y2?},{x3, y3?},{x4, y4?},............{xn, yn?}}

    not (-x1 + x2) y1 + (-x2 + x3) y2 + (-x3 + x4) y3

Using an interpolation data as high as 8 can lead to problems if there is noise in the data.

Example data.

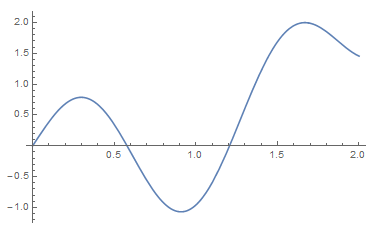
data1 = Table[{x, Sin[5 x] + x^2 - x}, {x, 0, 2, 0.1}]

(*{{0., 0.}, {0.1, 0.389426}, {0.2, 0.681471}, {0.3, 0.787495}, {0.4, 
  0.669297}, {0.5, 
  0.348472}, {0.6, -0.09888}, {0.7, -0.560783}, {0.8, -0.916802}, \
{0.9, -1.06753}, {1., -0.958924}, {1.1, -0.59554}, {1.2, -0.0394155}, \
{1.3, 0.60512}, {1.4, 1.21699}, {1.5, 1.688}, {1.6, 1.94936}, {1.7, 
  1.98849}, {1.8, 1.85212}, {1.9, 1.63485}, {2., 1.45598}}*)

Then Integrate data1

SS = Integrate[Interpolation[data1, InterpolationOrder -> 8][x], x];
m = 0.1; Sol = Table[{x, SS}, {x, 0, 2, m}]

(*{{0., 0.}, {0.1, 0.0198172}, {0.2, 0.0746065}, {0.3, 0.149853}, {0.4, 
  0.224563}, {0.5, 0.276896}, {0.6, 0.289999}, {0.7, 0.256625}, {0.8, 
  0.181395}, {0.9, 
  0.0801592}, {1., -0.023399}, {1.1, -0.103067}, {1.2, -0.136034}, \
 {1.3, -0.107984}, {1.4, -0.0161135}, {1.5, 0.130673}, {1.6, 
  0.314434}, {1.7, 0.513069}, {1.8, 0.706226}, {1.9, 0.880768}, {2., 
  1.03448}}*)

You can change "m" and "InterpolationOrder".

Check:

{NIntegrate[Sin[5 x] + x^2 - x, {x, 0, 2}], 
 NIntegrate[Interpolation[data1, InterpolationOrder -> 8][x], {x, 0, 2}]}
(*{1.03448, 1.03448}*)

Questions: 1.Yes. 2.You don't need them.They are marked as comments. (* "text" *)