How far did you proceed, Luis?

In case you want a job list, here it is. Co-ordinates come from the citation you gave Wearie-Phelan Bubbles

    (* Dodecahedron *)
    ddh = Partition[{3.1498, 0, 6.2996,
       -3.1498, 0, 6.2996,
       4.1997, 4.1997, 4.1997,
       0, 6.2996, 3.1498,
       -4.1997, 4.1997, 4.1997,
       -4.1997, -4.1997, 4.1997,
       0, -6.2996, 3.1498,
       4.1997, -4.1997, 4.1997,
       6.2996, 3.1498, 0,
       -6.2996, 3.1498, 0,
       -6.2996, -3.1498, 0,
       6.2996, -3.1498, 0,
       4.1997, 4.1997, -4.1997,
       0, 6.2996, -3.1498,
       -4.1997, 4.1997, -4.1997,
       -4.1997, -4.1997, -4.1997,
       0, -6.2996, -3.1498,
       4.1997, -4.1997, -4.1997,
       3.1498, 0, -6.2996,
       -3.1498, 0, -6.2996}, 3]


(* Tetrakaidecahedron *)
tkh = Partition[{3.14980, 3.70039, 5,
   -3.14980, 3.70039, 5,
   -5, 0, 5,
   -3.14980, -3.70039, 5,
   3.14980, -3.70039, 5,
   5, 0, 5,
   4.19974, 5.80026, 0.80026,
   -4.19974, 5.80026, 0.80026,
   -6.85020, 0, 1.29961,
   -4.19974, -5.80026, 0.80026,
   4.19974, -5.80026, 0.80026,
   6.85020, 0, 1.29961,
   5.80026, 4.19974, -0.80026,
   0, 6.85020, -1.29961,
   -5.80026, 4.19974, -0.80026,
   -5.80026, -4.19974, -0.80026,
   0, -6.85020, -1.29961,
   5.80026, -4.19974, -0.80026,
   3.70039, 3.14980, -5,
   0, 5, -5,
   -3.70039, 3.14980, -5,
   -3.70039, -3.14980, -5,
   0, -5, -5,
   3.70039, -3.14980, -5}, 3]

display them with

ConvexHullMesh[ddh]
ConvexHullMesh[tkh]

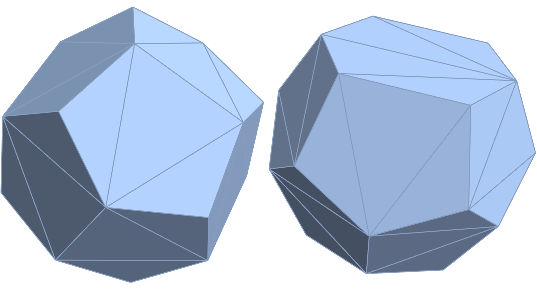
visit elements (2-faces, 1-faces (edges), 0-faces (points))

MeshCells[ConvexHullMesh[ddh], 2]
MeshCells[ConvexHullMesh[tkh], 1]

Now

• have list of faces of the ddh and a list of faces of tkh which fit together to make up the bubble
• have a list of glueing faces of the bubble (face and what fits to it)
• take one (a ddh or a tkh) as starting polyhedron of the bubble
• select one of the glueing faces by random
• use FindGeometricTransform to bring the next polyhedron (of the fitting type) into fitting position
• update the list of glueing faces of the bubble
• repeat the last three steps as long as it pleases you
• don't forget to rotate the bubble (and the corresponding lists)
• mind a bit about data structures (otherwise it can become rather painful)

Written that way it will possibly not flow like a movie because of the continous use of FindGeometricTransform, but that's it already. Later on you can replace FindGeometricTransform with a set of explicit translations and rotations for the cases at hand.

It will be quite a bit harder to let the next polyhedron fly from a store at a fixed place into fitting position on the rotating bubble.

After trying to build the structure of weire and phelam following some steps that i invented based on the page that i shared earlier, I have to say clearly that I am not very happy with the results obtained, by which i went back to search again on the internet for some new idea and I was pleasantly surprised to see that the structure is made in grasshopper as you can see on the following link, weaire phelan using grasshopper

you will recall that there is a video where Cris Carlson shows that you can use Mathematica and grasshopper together, the problem is that I do not know if there is a file of grasshopper that contains information on how to make this structure and if someone can help me do that in Mathematica. Waiting for any kind of help on your part,

I say goodbye wishing him all an excellent day.

In a general form those structures should be the result of VoronoiMesh for the 3D case. The documentation ("Details and Options") says:

The cells will be intervals in 1D, convex polygons in 2D, and convex polyhedra in 3D.

Consequently the 3D case should be feasible, but I could not make that work. I defininitely would like to know how to do that.

Regards -- Henrik