In the process of developing
some demonstrations I published recently about bisecting the perimeter of triangles I came across the following result. Consider the arc AB of a circle, the segment AB not necesarily being a diameter of the circle. If M is the apex in the middle of the arc and we join it to the center N of AB, then clearly AN = BN. In other words, if we join the middle M of arc AB with the middle N of segment AB, segments MN and AB are perpendicular and AN = BN. Perhaps the following manipulate would clarify the idea.
Manipulate[
Block[{r}, r = Sqrt[1 + h^2];
{c1, c2} = If[h < 0, {6, 5}, {5, 6}];
Graphics[{{EdgeForm[Thick], ColorData[2, c1], Disk[{0, -h}, r],
ColorData[2, c2],
Disk[{0, -h}, r, {ArcTan @@ {1, h}, ArcTan @@ {-1, h}}]},
ColorData[2, c1], Rectangle[{-1, -h}, {1, 0}], Black,
Line[{{-1, 0}, {1, 0}}], Line[{{0, -h + r}, {0, 0}}],
Style[{Text["A", {-1, -.1}], Text["B", {1, -.1}],
Text["M", {0, -h + r + .1}], Text["N", {0, -.1}]}, 20, Bold]},
PlotRange -> 1.2]],
{{h, 0, "circle"}, -1, 2, Slider}]
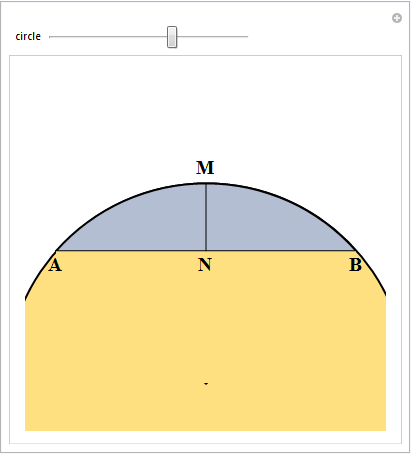
Now for the interesting part. Suppose that there is a point C on the arc AB and instead of defining N as the perpendicular from M to AB, we take N as the perpendicular from M to AC and now relabel as D the middle point of segment AB (if point C is at the left of M we take N to be the perpendicular from M to BC). The following manipulate illustrates this.
Manipulate[
r = Sqrt[1 + h^2];
al = If[h == 0, Pi/2, ArcTan[1/h]];
a = If[h > 0, {al - Pi/2,
3 Pi/2 - al}, {Pi/2 - al, Pi/2 + al}];
ac = cc Last[a] + (1 - cc) First[a];
c = {0, h} + r {Cos[ac], Sin[ac]};
n = If[First[c] > 0, {-1, 0} +
Projection[{1, h + r}, c + {1, 0}], {1, 0} +
Projection[{-1, h + r}, c - {1, 0}]];
Graphics[{EdgeForm[Thick],
Circle[{0, h}, r, a], Black, Line[{{-1, 0}, c, {1, 0}, {-1, 0}}],
Line[{{0, h + r}, n}],
Style[{Text["A", {-1, -.1}], Text["B", {1, -.1}],
Text["M", {0, h + r + .1}], Text["D", {0, -.1}], Text["C", c],
Text["N", n]}, 20, Bold]},
PlotRange -> {{-1.5, 1.5}, {-.2, 2.5}}],
{{h, 0, "circle"}, -3, .9, Slider},
{{cc, .3, "point C"}, 0, 1, Slider}]
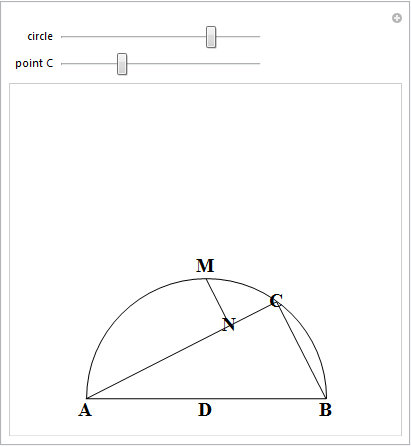
Surprisingly, considering lengths, AN = NC + CB (or BN=NC+AC if C is to the left of M). Perhaps some reader can come up with a proof of this result?. What has this to do with bisecting perimeters of triangles and what is the importance of point D to even having received a label? Well, it turns out that the segment DN bisects the perimeter of triangle ABC.
In seeking for an algebraic proof of this result, we set a = (1, 0), b = (-1, 0), d=(0,0) and the center of the circle at (0, h) with variable h. The radius of the circle is then r = Sqrt[1 + h^2]. Thus m = (0, h + r) and c = (0, h) + r (cos (t), sin (t)) for some value of t not exceeding pi/2 (the other bound will be mentioned later).
The point n is then obtained as
{a, b} = {{-1, 0}, {1, 0}};
r = Sqrt[1 + h^2];
m = {0, h + r};
c = {0, h} + r {Cos[t], Sin[t]};
n = FullSimplify[a + (m - a).(c - a) (c - a)/((c - a).(c - a))]
{1/2 (-1 + (h + Sqrt[1 + h^2]) Cos[t] + Sin[t]), 1/2 (-Cos[t] + (h + Sqrt[1 + h^2]) (1 + Sin[t]))}
With these values, the expression we want to verify being equal to zero is tested as:
FullSimplify[Norm[n - a] - Norm[n - c] - Norm[c - b] /. Abs[xx_]^2 -> xx^2, t < Pi/2]
-Sqrt[(-1 + h (-h + Sqrt[1 + h^2])) (-1 + Sin[t])] + Sqrt[(1 +
h (h + Sqrt[1 + h^2])) (1 + Sin[t])] -
Sqrt[2] Sqrt[1 + h^2 + Sqrt[1 + h^2] (-Cos[t] + h Sin[t])]
So, we are left with the following (probably) true theorem

but this takes us further away from the proof we want.