I'm trying to solve this differential equation in elliptic coordinate system:
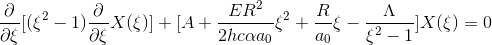
My real problem is inserting the physical boundary condition that makes the function a well behavior one, and obtaining the analytical solution in Wolfram Mathematica. Using DSolve I got a differential root witch means that the solution should be numerical but I'm sure this is not my case. I'm asking you how can I solve this kind of differential equation in Mathematica with an analytical solution.