Here is the integer programming method to force a minimum on the number of inequalities violated. The code is almiost the same as before except we make the objective function use 0-1 variables. The 10^6 usage is a heuristic. In general we want something with a quotient much larger than a machine precision ULP, but smaller than the max violation (else we'll have an unsatisfiable system). Stated differently, the result will be optimal unless there is a consistent system from omitting fewer inequalities but accepting a constraint violation larger than 10^6.

e2 = eqs /. {aa_ >= bb_ :> bb - aa, aa_ <= bb_ :> aa - bb};
cvars = Array[c, Length[e2]];
ineqs1 = Thread[cvars >= e2/10^6];
ineqs2 = Thread[0 <= cvars <= 1];
obj = Total[cvars];
allvars = Join[cvars, Variables[e2]];

In[205]:= NMinimize[{obj, 
  Join[ineqs1, ineqs2, {Element[cvars, Integers]}]}, allvars]

(* Out[205]= {2., {16[1] -> 0, 16[2] -> 1, 16[3] -> 0, 16[4] -> 0, 
  16[5] -> 0, 16[6] -> 0, 16[7] -> 0, 16[8] -> 0, 16[9] -> 0, 
  16[10] -> 0, 16[11] -> 0, 16[12] -> 1, 16[13] -> 0, 16[14] -> 0, 
  16[15] -> 0, 16[16] -> 0, 16[17] -> 0, 16[18] -> 0, 16[19] -> 0, 
  16[20] -> 0, 16[21] -> 0, 16[22] -> 0, 16[23] -> 0, 16[24] -> 0, 
  16[25] -> 0, 16[26] -> 0, 16[27] -> 0, 16[28] -> 0, 16[29] -> 0, 
  16[30] -> 0, x -> 38.7097, y -> 92.4653882578, z -> -1.07476935423}} *)

I will remark that this particular solution gives a worse total violation than my previous one, but only requires removal of two inequalities (#2 and #12; this time it's not a matter of checking by eyeball). Also I will say that this approach can be slow in general, although in this example it is quite fast.

OK, I got it. "Hinreichende Bedingung"! This is a good starting point for my problem. So I can scan my several hundred equation systems for possible issues. Thanks a lot.

Dear Daniel,

thanks a lot for your work; I have tested this with a few equations. However, your code will also flag equation 27 in my example above, right? If I just eliminate equations 2, 12 and leave 27, I can solve the system using Reduce and Solve.

How should I interpretate your solution? Do I need to remove 2, 12 and 27 to get a solvable system?

Hi Andreas,

this is an interesting problem and I would like to see a definitive answer as well!

One gets an idea about the nature of the problem by playing around. You can start with searching for pairwise conflicts:

pIndexList2 = Select[Tuples[Range[Length[eqs]], 2], First[#] < Last[#] &];
comb2 = Select[{{#1, #2}, FullSimplify[eqs[[#1]] && eqs[[#2]]]} & @@@ pIndexList2, ! #[[2]] &]
(*   Out:  {{{12,13},False}}  *)

In the same manner one can find conflicting triples:

pIndexList3 = Select[Tuples[Range[Length[eqs]], 3], #[[1]] < #[[2]] < #[[3]] &];
comb3 = Select[{{#1, #2, #3}, FullSimplify[eqs[[#1]] && eqs[[#2]] && eqs[[#3]]]} & @@@ pIndexList3, ! #[[2]] &];
comb3 /. {{___, 12, 13, ___}, _} -> Nothing  (* new combinations only *)
(* Out:  {{{1,2,27},False},{{1,12,27},False},{{2,11,27},False},{{11,12,27},False}}  *)

or quadruples:

pIndexList4 = Select[Tuples[Range[Length[eqs]], 4], #[[1]] < #[[2]] < #[[3]] < #[[4]] &];
comb4 = Select[{{#1, #2, #3, #4}, FullSimplify[eqs[[#1]] && eqs[[#2]] && eqs[[#3]] && eqs[[#4]]]} & @@@ 
    pIndexList4, ! #[[2]] &];
falseCombsPattern = {#, _} & /@ {{___, 12, 13, ___}, {1, 2, ___, 27, ___}, {1, ___, 12, ___, 27, ___}, {___, 2, ___, 11, ___, 27, ___}, {___, 11, 12, ___, 27, ___}};
comb4 /. Thread[falseCombsPattern -> Nothing]  (*  new combinations only  *)

For me the interesting point seems to become obvious by making a statistics of the indices of all quadruples:

ListPlot[Tally@Flatten[First /@ comb4], PlotRange -> All]

giving:

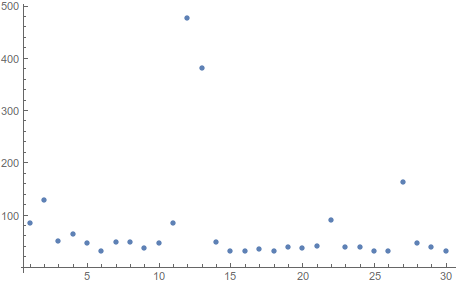
So my guess is that the most conflicting equations are always the ones which gives a pairwise conflict (eqn12 and eqn13 in this case), because they show up in all other combinations as well. Then in this ranking comes eqn27 and then eqn2. Does that make sense to you?

Regards -- Henrik