Look at this picture of a semi-circular fan spanning 120 degrees having a variety of internal tangential circles.
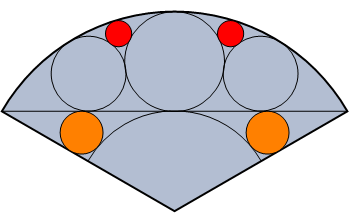
Now, ponder the following question : If the radius of the orange circle is 1, what is the value of the radius of the red circle?
My reference (The Math Book - Pickover) mentioned many things that intrigued me, among those the following : The answer is
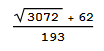
This problem was created and solved by an 11-year-old boy in Japan in 1873 and his creation was commited to a wood tablet in a temple!.
So I was motivated to use Mathematica to arrive at the answer. Let us change the picture and label point a:
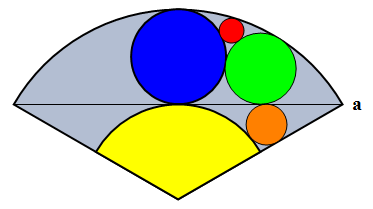
Let us now refer only to the circles appearing in the above picture by their colors.
Let (x1, y1) be the center of orange (we know its radius is 1), (x2, y2) and r2 the corresponding to the center and radius of green and (x3, y3) and r3 those of red. We want the value of r3.
Assume the enclosing circle forming the fan - which we will call cyan - has its centre at the origin and it is of radius r.
Then yellow has radius r/2 and blue has radius r/4. And a = r/2 (Sqrt[3], 1).
There are three conditions orange has to fullfil corresponding to its three tangencies. One of them corresponds to the formula of the distance of a point to a line, the point being (x1, y1) and the line being that of slope 1/Sqrt[3] joining the origin with point a. The following Solve includes the three conditions
Simplify[Solve[{y1 == r/2 - 1, Norm[{x1, y1}] == r/2 + 1, 1 == (y1 - 1/Sqrt[3] x1)/Sqrt[1 + 1/3]}, {x1, y1, r}]]
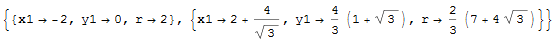
We need the second solution (can you spot what circle indicates the first solution?) So,
{x1, y1, r} = {2 + 4/Sqrt[3], 4/3 (1 + Sqrt[3]), 2/3 (7 + 4 Sqrt[3])};
Similarly, green obeys three tangencies: to the horizontal line, to cyan and to blue. The following Solve handles them
Simplify[Solve[{y2 == r/2 + r2, Norm[{x2, y2}] == r - r2,Norm[{x2, y2} - {0, 3 r/4}] == r/4 + r2}, {x2, y2, r2}]]
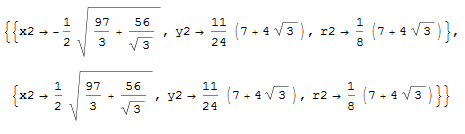
so we set
{x2, y2, r2} = {1/2 Sqrt[97/3 + 56/Sqrt[3]] , 11/24 (7 + 4 Sqrt[3]),
1/8 (7 + 4 Sqrt[3])};
Finally, red is tangent to cyan, blue and green :
FullSimplify[{x3, y3, r3} /.
Solve[{Norm[{x3, y3} - {0, 3 r/4}] == r/4 + r3,
Norm[{x3, y3} - {x2, y2}] == r2 + r3,
Norm[{x3, y3}] == r - r3}, {x3, y3, r3}]]
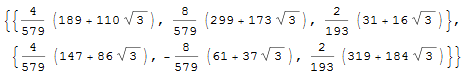
(can you spot where is the circle corresponding to the second one of the above solutions?). Finally, we checked our answer with the one in the book:
(Sqrt[3072] + 62)/193 == 2/193 (31 + 16 Sqrt[3])
True
What strikesme was not only that a boy in Japan knew about 150 years ago how to solve non -linear systems of equations. I think his talent had nothing to do with these kind of habilities but in having the imagination to pose the problem in the first place and to carry on and publish it under so difficult circumstances, hability that is still impressive nowadays.