Did you know the following avatar of Pythagoras theorem?. Consider a right-angled triangle of catheti (Greek work plural of cathetus, meaning each of the sides forming the vertex with the right angle) of lengths a and b. Let h be the length of the height connecting this vertex to the hypotenuse (largest side). Then a, b and h are related as:
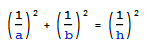
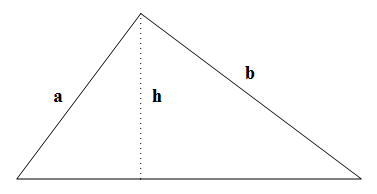
calling c the length of the hypotenuse, we verify the result as follows (what is d standing for in the conditions?)
FullSimplify[
Eliminate[{h^2 + d^2 == a^2, h^2 + (c - d)^2 == b^2,
c^2 == a^2 + b^2}, {c, d}] /. {a -> 1/A, b -> 1/B, h -> 1/H}, {A >
0, B > 0, H > 0}]
A^2 + B^2 == H^2
Initially, I tried the following but the one above was more emphatic.
FullSimplify[
Eliminate[{h^2 + d^2 == a^2, h^2 + (c - d)^2 == b^2,
c^2 == a^2 + b^2}, {c, d}], {a > 0, b > 0, h > 0}]
a^2 b^2 == (a^2 + b^2) h^2
So, next time somebody asks you to draw a (3, 4, 5) right triangle, choosing to join the points (0, 0), (3, 0), (3, 4) (or (0, 0), (4, 0), (4, 3)) would not do if the triangle is placed in the above position. It turns out that the coordinates can be set all to be rational numbers. Or can be scaled so that the coordinates are all integer numbers! In our example, (0, 0), (25, 0) and (9, 12).
Joke: have you heard of the (1/3, 1/4, 1/5) right triangle? (a, b, h) = (1/3, 1/4, 1/5).
If instead of squares we consider square roots we have another striking equation
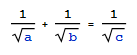
it corresponds to the radius of the circles in the following configuration
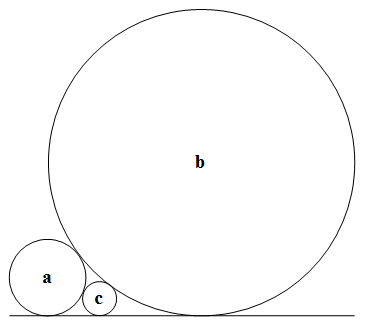
Can you find an example of integral values for a, b and c? . Hint : 1/3 + 1/6 = 1/2 and it is the one depicted above. Can you find different non-square integral values?. Hint, consider any of the following
Select[Flatten[
Table[{a, b, (Sqrt[a b]/(Sqrt[a] + Sqrt[b]))^2}, {a, 500}, {b,
a + 1, 500}], 1],
IntegerQ[Last[#]] \[And] (! IntegerQ[Sqrt[First[#]]]) &]
{{18, 72, 8}, {27, 108, 12}, {32, 288, 18}, {45, 180, 20}, {48, 432,
27}, {54, 216, 24}, {63, 252, 28}, {72, 288, 32}, {90, 360,
40}, {99, 396, 44}, {108, 432, 48}, {117, 468, 52}, {200, 450, 72}}
Finally, what is the equation behind the following equalities?
Map[Row[{"1 = ", Row[Riffle[1/#, "+"]]}] &,
NestList[Flatten[{Most[#], Last[#] + 1,
Last[#] (Last[#] + 1)}] &, {1}, 8]] // Column
