Hi everyone. Any help is appreciated. Here is my problem. I need to maximize the largest eigenvalue of square matrix (looking for spectral radius). Matrix elements depend on the integral of the product of two associated Legendre functions in numerator and optimization parameter in denominator as follows:
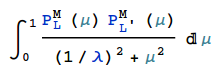
In my code (below) I use NMaximize option to find global maximum over lambda. In all the examples I could find in Mathematica Help this maximization procedure is used only with explicitly defined functions, but not like in my case with the optimization parameter in the integrand. Optimization procedure complains about evaluating integral to non-numerical value without giving any result. Strangely enough, I can easily plot the eigenvalue over optimization parameter by substituting NMaximize with Plot . Symbolic integration is not practical already for 3 by 3 matrix. Any ideas how to overcome this difficulty? Thanks. I use Mathematica 10.0.2.0.
M = 0;
Lmax = 2;
NMaximize[
Max[Abs[Eigenvalues[
Table[If[
Mod[i + j, 2] == 0, (1/\[Lambda])^2*
NIntegrate[(
LegendreP[i, M, x]*LegendreP[j, M, x])/((1/\[Lambda])^2 +
x^2), {x, 0, 1}], (1/\[Lambda])*
NIntegrate[(
x*LegendreP[i, M, x]*LegendreP[j, M, x])/((1/\[Lambda])^2 +
x^2), {x, 0, 1}]], {i, M, Lmax}, {j, M, Lmax}]]]], \[Lambda]]