Message Boards Message Boards

Could you tell me what am I doing wrong?

Luis Ledesma
Posted 9 years ago

Again sharing my problems, sharing information with some friends one of them i shared this code in Matlab and try to do the same in Mathematica, i found myself with the unpleasant surprise that don't know if the function ArrayResample do the same as the function interp2 Matlab,the code is short and my attempt to do the same in Mathematica is the following. 

    terre = ConstantArray[0, {2, 2}];
      c = 0.1;
For[i = 1, i < 7, i++,
 ele = Length[terre];
 nLon = 2*ele - 1;
 (*paso B*)terre = ArrayResample[terre, nLon];
 subsquares = ConstantArray[1, Dimensions[terre]];
 subsquares[[1 ;; Length[subsquares] ;; 2, 
   1 ;; Length[subsquares] ;; 2]] = 0;
 vals = Position[subsquares, 1];
 randmap = c*RandomVariate[NormalDistribution[], Dimensions[terre]];
 rval = Extract[randmap, vals];
 camb = Thread[vals -> rval];
 terre = ReplacePart[terre, camb];
 c = c/2;
 ]

The attached file in Matlab for you tell me some idea of why the chart does not i get equal.

Here is the graphics obteined with mathematica

ListPlot3D[terre, Mesh -> None, Boxed -> False, Axes -> False, 
 ColorFunction -> ColorData["Rainbow"], DataRange -> {{0, 1}, {0, 1}},
  Background -> GrayLevel[.1]]

But you should see a graph like this, here is the graph.

I want one like this

Attachments:
POSTED BY: Luis Ledesma
6 Replies
Sort By:
Luis Ledesma
Luis Ledesma
Posted 9 years ago

Hi UDO KRAUSE , thanks for to go further into the matter, the truth you've contributed a lot to improve the appearance of graphs that are obtained, run your code and my machine only able to support up to the iteration 8 for plotting, already that when trying to plot the iteration 9 took too long, but your code for the construction of terre remains amazing and short,thank you for sharing your improvements, I hope that someone else also enjoy this marvel.Sincerely Luis
POSTED BY: Luis Ledesma

This gives reasonably grid-non-artificial landscapes

Remove[pic, c, terre, subsquares] 
With[{endIt = 10},
 terre = ConstantArray[0, {2, 2}]; c = 0.1; 
 For[i = 1, i < endIt, i++, ele = Length[terre]; 
  nLon = 2*ele - 1;(*paso B*)terre = ArrayResample[terre, nLon]; 
  subsquares = ConstantArray[1, Dimensions[terre]]; 
  subsquares[[
    1 ;; Length[subsquares] ;; 
     RandomChoice[Range[2, Ceiling[Length[subsquares]/2]]], 
    1 ;; Length[subsquares] ;; 
     RandomChoice[Range[2, Ceiling[Length[subsquares]/2]]]]] = 0; 
  vals = Position[subsquares, 1]; 
  randmap = c*RandomVariate[NormalDistribution[], Dimensions[terre]]; 
  rval = Extract[randmap, vals]; camb = Thread[vals -> rval]; 
  terre += ReplacePart[terre, camb]; pic[i] = terre; c = c/2
  ]
 ]

it is Luis' code with one more modification on placing zeroes.

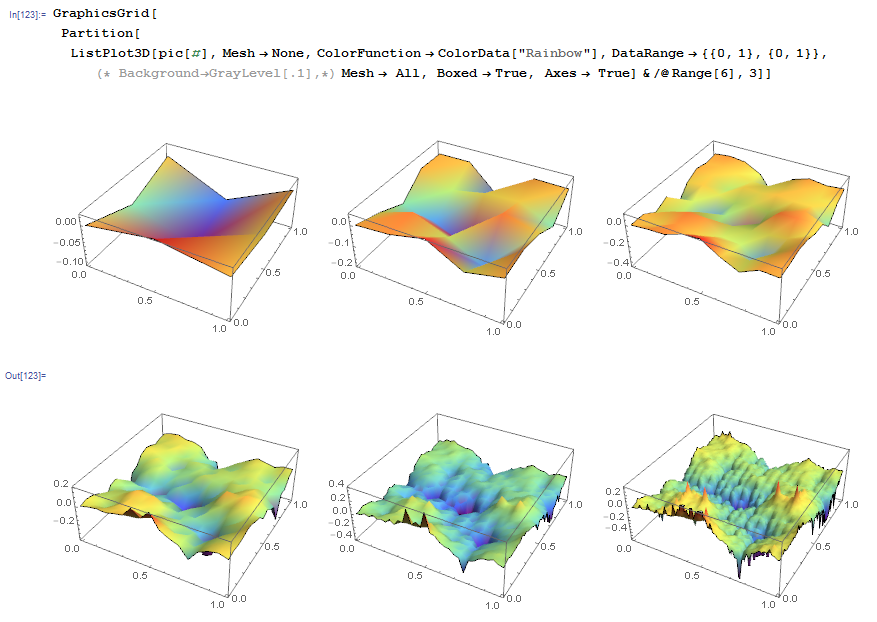
enter image description here
POSTED BY: Udo Krause

To cure this, one could do

ledesmaSpec[{a_, f_, x0_, y0_}, x_, y_] := a Cos[f Sqrt[(x - x0)^2 + (y - y0)^2]] Exp[-Sqrt[(x - x0)^2 + (y - y0)^2]]

Clear[freqs]
With[{len = 17},
 freqs = Transpose[{RandomReal[{-2, 2}, len], RandomReal[5 \[Pi], len], RandomReal[1, len], RandomReal[1, len]}];
 ]

Plot3D[Plus @@ (ledesmaSpec[#, x, y] & /@ freqs), {x, 0, 1}, {y, 0, 1}, 
 ColorFunction -> ColorData["Rainbow"], Background -> GrayLevel[.1], Mesh -> None]

to see

enter image description here

note that freqs has all random real selectors executed only once. To let it appear not so smooth, trench it with a random real which is evaluated during graphics construction

Plot3D[Plus @@ (ledesmaSpec[#, x, y] & /@ freqs) + RandomReal[0.1], {x, 0, 1}, {y, 0, 1}, 
 ColorFunction -> ColorData["Rainbow"], Background -> GrayLevel[.1], Mesh -> None]

enter image description here

It's still a bit artificial, you could also add an inclined plane to give it a tendency.
POSTED BY: Udo Krause

Let's modestly say it did improve. But if one looks from above onto it

enter image description here

one sees the rectangular subsquare structure, which is still artificial.
POSTED BY: Udo Krause
Luis Ledesma
Luis Ledesma
Posted 9 years ago

Udo Krause, that great help you have given me, with what you have showed me and corrected I have remained convinced in the result, thank you very much, without your help it would not have been possible, I like very much the images that are obtained.

Greetings Luis Ledesma :)
POSTED BY: Luis Ledesma

Store the intermediate values of terre on an associative array pic and plot it at the end to see what happened:

Remove[pic, c, terre, subsquares]
terre = ConstantArray[0, {2, 2}];
c = 0.1;
For[i = 1, i < 7, i++, ele = Length[terre]; nLon = 2*ele - 1;(*paso B*)
 terre = ArrayResample[terre, nLon]; 
 subsquares = ConstantArray[1, Dimensions[terre]]; 
 subsquares[[1 ;; Length[subsquares] ;; 2, 
    1 ;; Length[subsquares] ;; 2]] = 0; 
 vals = Position[subsquares, 1]; 
 randmap = c*RandomVariate[NormalDistribution[], Dimensions[terre]]; 
 rval = Extract[randmap, vals]; camb = Thread[vals -> rval]; 
 terre = ReplacePart[terre, camb];
 pic[i] = terre;
 c = c/2
 ]

GraphicsGrid[
 Partition[
  ListPlot3D[pic[#], Mesh -> None, 
     ColorFunction -> ColorData["Rainbow"], 
     DataRange -> {{0, 1}, {0, 1}},(* Background\[Rule]GrayLevel[.1],*) 
     Mesh -> All, Boxed -> True, Axes -> True] & /@ Range[6], 3]]

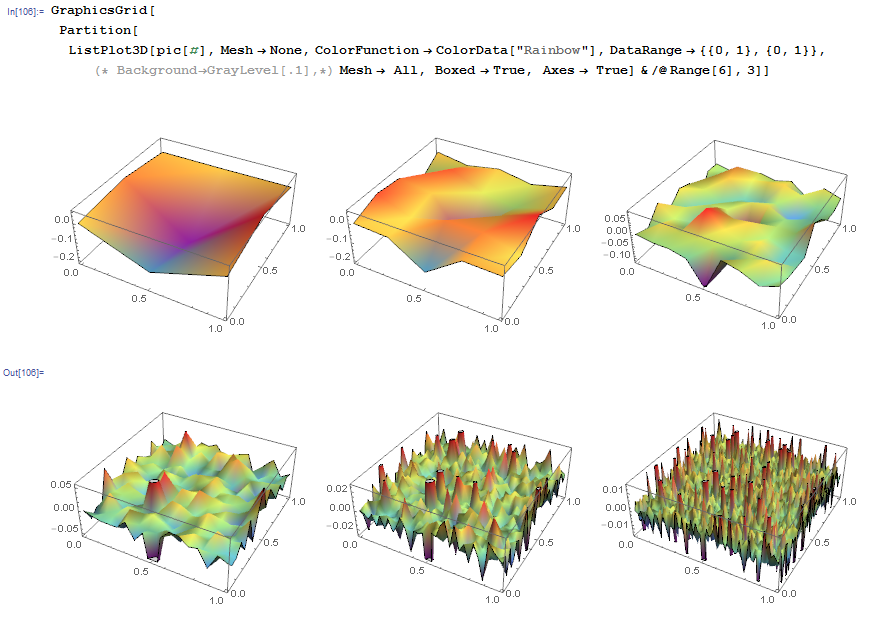
enter image description here

you seem to refine and damp the perturbations again and again around 0 terrain level. If instead you respect the previous terre by adding the new one on it

Remove[pic, c, terre, subsquares]
terre = ConstantArray[0, {2, 2}];
c = 0.1;
For[i = 1, i < 7, i++, ele = Length[terre]; nLon = 2*ele - 1;(*paso B*)
 terre = ArrayResample[terre, nLon]; 
 subsquares = ConstantArray[1, Dimensions[terre]]; 
 subsquares[[1 ;; Length[subsquares] ;; 2, 
    1 ;; Length[subsquares] ;; 2]] = 0; 
 vals = Position[subsquares, 1]; 
 randmap = c*RandomVariate[NormalDistribution[], Dimensions[terre]]; 
 rval = Extract[randmap, vals]; camb = Thread[vals -> rval]; 
 terre += ReplacePart[terre, camb];
 pic[i] = terre;
 c = c/2
 ]

it looks far more natural:

enter image description here
POSTED BY: Udo Krause
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract