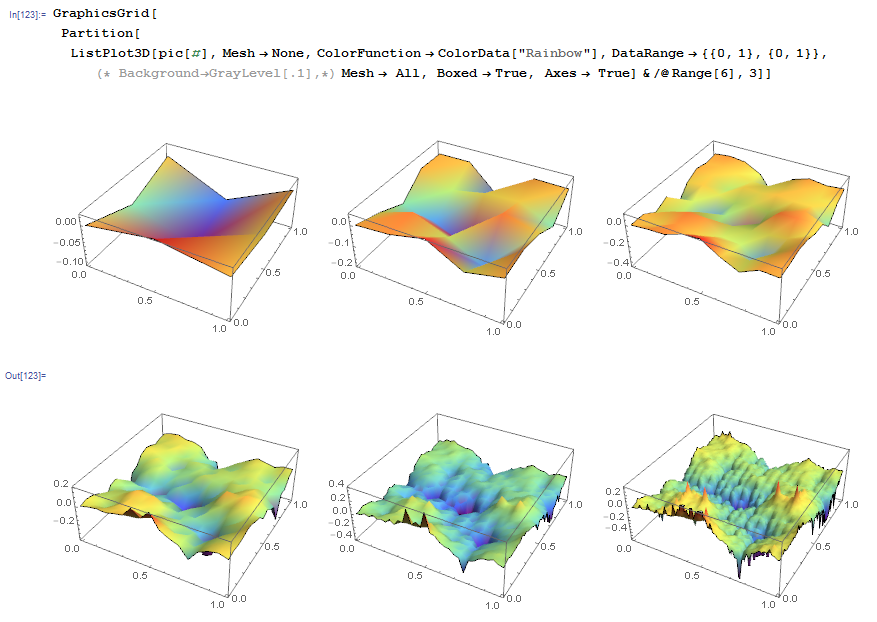
Store the intermediate values of terre on an associative array pic and plot it at the end to see what happened:
Remove[pic, c, terre, subsquares]
terre = ConstantArray[0, {2, 2}];
c = 0.1;
For[i = 1, i < 7, i++, ele = Length[terre]; nLon = 2*ele - 1;(*paso B*)
terre = ArrayResample[terre, nLon];
subsquares = ConstantArray[1, Dimensions[terre]];
subsquares[[1 ;; Length[subsquares] ;; 2,
1 ;; Length[subsquares] ;; 2]] = 0;
vals = Position[subsquares, 1];
randmap = c*RandomVariate[NormalDistribution[], Dimensions[terre]];
rval = Extract[randmap, vals]; camb = Thread[vals -> rval];
terre = ReplacePart[terre, camb];
pic[i] = terre;
c = c/2
]
GraphicsGrid[
Partition[
ListPlot3D[pic[#], Mesh -> None,
ColorFunction -> ColorData["Rainbow"],
DataRange -> {{0, 1}, {0, 1}},(* Background\[Rule]GrayLevel[.1],*)
Mesh -> All, Boxed -> True, Axes -> True] & /@ Range[6], 3]]
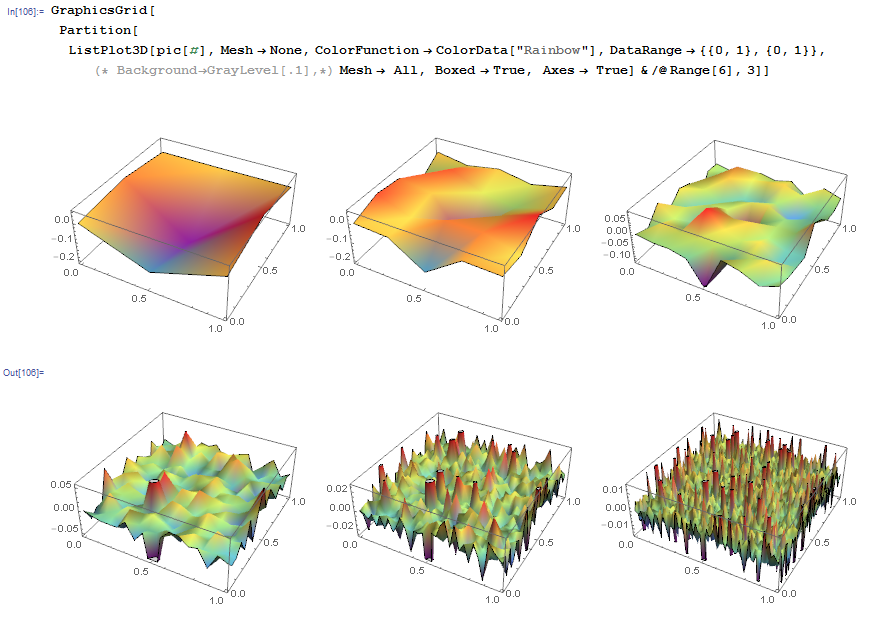
you seem to refine and damp the perturbations again and again around 0 terrain level. If instead you respect the previous terre by adding the new one on it
Remove[pic, c, terre, subsquares]
terre = ConstantArray[0, {2, 2}];
c = 0.1;
For[i = 1, i < 7, i++, ele = Length[terre]; nLon = 2*ele - 1;(*paso B*)
terre = ArrayResample[terre, nLon];
subsquares = ConstantArray[1, Dimensions[terre]];
subsquares[[1 ;; Length[subsquares] ;; 2,
1 ;; Length[subsquares] ;; 2]] = 0;
vals = Position[subsquares, 1];
randmap = c*RandomVariate[NormalDistribution[], Dimensions[terre]];
rval = Extract[randmap, vals]; camb = Thread[vals -> rval];
terre += ReplacePart[terre, camb];
pic[i] = terre;
c = c/2
]
it looks far more natural: