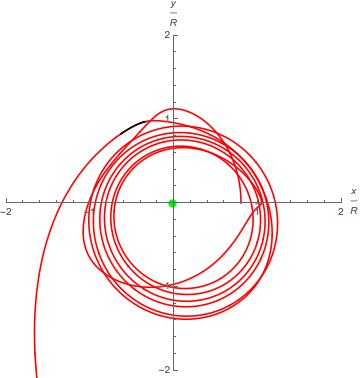
I am in the beginning stages of my project of modeling earth-moon-satellite system.I was able to plot my solution but now i want to animate it, I have never used animate and I am confused on making this animation. Can someone show me how i would go about doing this? I wanna make a slider bar from time 0 to 50.

G = 6.67*10^-11;
Subscript[m, e] = 5.97*10^24;
Subscript[m, m] = 7.35*10^22;
r = 385000000;
Subscript[d, 1] = 
  Subscript[m, m]/(Subscript[m, m] - Subscript[m, e])*r;
Subscript[d, 2] = r + Subscript[d, 1];
Subscript[m, 1] = Subscript[m, e]/(
  Subscript[m, e] + Subscript[m, m]);
Subscript[m, 2] = Subscript[m, m]/(
  Subscript[m, e] + Subscript[m, m]);
d1 = Subscript[m, 2];
d2 = Subscript[m, 1];
Subscript[r, e] = 6371000;
Subscript[r, m] = 1737000;

I have solved the differential equation already.

s7 = NDSolve[{x''[
     t] == -(Subscript[m, 
        1]/((x[t] + d1*Cos[t])^2 + (y[t] + d1*Sin[t])^2)^(3/
        2) (x[t] + d1*Cos[t]) + 
       Subscript[m, 2]/((x[t] - d2*Cos[t])^2 + (y[t] - d2*Sin[t])^2)^(
        3/2) (x[t] - d2*Cos[t])), 
   y''[t] == -((
       Subscript[m, 
        1] (y[t] + 
          d1*Sin[t]))/((x[t] + d1*Cos[t])^2 + (y[t] + d1*Sin[t])^2)^(
       3/2) + (Subscript[m, 
        2] (y[t] - 
          d2*Sin[t]))/((x[t] - d2*Cos[t])^2 + (y[t] - d2*Sin[t])^2)^(
       3/2)), x'[0] == 0, y'[0] == 1.3, x[0] == .8, y[0] == 0}, {x, 
   y}, {t, 50}]

I was able to get this plot to show. How can it be animated.

Show[{Graphics[{Green, 
    Disk[{-d1*Cos[0], -d1*Sin[0]}, 3 Subscript[r, e]/r], Gray, 
    Disk[{d2*Cos[0], d2*Sin[0]}, 3 Subscript[r, m]/r]}], 
  ParametricPlot[Evaluate[{x[t], y[t]} /. s7], {t, 0, 50}, 
   PlotStyle -> Red], 
  ParametricPlot[Evaluate[{x[t], y[t]} /. s7], {t, 45.9, 46.1}, 
   PlotStyle -> Black]}, PlotRange -> {{-2, 2}, {-2, 2}}, 
 Axes -> True, 
 AxesLabel -> {"\!\(\*FractionBox[\(x\), \(R\)]\)", 
   "\!\(\*FractionBox[\(y\), \(R\)]\)"}]