Chemical stoichiometry is really a kind of homological algebra. I was able to implement at least a simple form of this using John Browne's Grassmann algebra code. There is a chain complex going from moieties (atoms or unbroken chemical units) to reactants to reactions. The boundaries of reactions are reactants and the boundary of reactants are moieties. If one writes the boundaries correctly then the boundary of a boundary is zero - and this corresponds to balancing chemical equations. I'll just display the key results.

The moieties for the problem are:

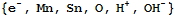
The reactants, which include several of the moieties, are:

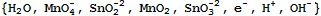
The boundary rules for the reactants essentially pull back the reactants to moieties. They are:

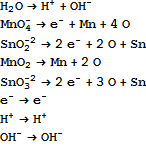
We pull back a generic reaction equation to moieties. That gives a set of equations for balance. We feed them to Mathematica to Solve. We obtain a two parameter solution, which means we have two independent reaction equations. They are:

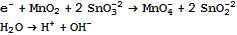
You are probably interested only in the first one. One neat feature of Mathematica, by the way, is that if you write these equations in the form something == 0, and then Simplify, Mathematica automatically segregates the terms so they are positive on both sides of the equal sign so all you have to do is change it to an arrow to get a chemical equation.

Thanks for your reply Daniel.

When you balance a redox reaction, you have to know whether the solution is acidic (H+) or alkaline (OH-). That will determinate if you have to balance the equation with H+ ions or OH- ions. If I just enter the chemical equation:

MnO4^- + SnO2^-2 = MnO2 + SnO3^-2

Then Wolfram does not know how to balance the redox reaction. How can I tell the computer to balance a redox reaction, and at the same time tell it, that the solution is acidic or alkaline in the input field?

Thanks!