Hi!
Lately I have been working a lot with simulations within the process industry. There, process operators often rely on years upon years of practical experience to know which parameters to tune to get optimal system performance. The relationship between the control signals manipulated by the operators and the desired response signals are often dynamical in nature where time constants can be longer than an hour. This can make it very hard to get a feeling for how changes made in one time instant will affect the process down the line, especially when multiple signals are being manipulated simultaneously.
Having a dynamical model that represents an industrial process can allow you to try out different scenarios before implementing them live. Using SystemModeler and Mathematica, one can take that process a step further and make continuous predictions based on updated values from the industrial process. These can both include predictions on where we are currently headed based on our current estimated system state and test based predictions where we manipulate a control signal and estimate how the system will evolve. Here, I will present a Mathematica notebook that is able to do just that, combined with a user interface that allows for testing of control signals. The Notebook and the Modelica models used can be downloaded at the bottom of this post.
For demonstration purposes, I created a purely fictitious process where the response was modeled as a sum of five transfer function responses. Nasser M. Abbasi in this thread showed an excellent way to generate transfer functions in a way that is compatible with the function RandomReal while allowing for only stable systems to be generated (i.e. only generating systems where poles have negative real parts). Simulations with a unit step input signal using OutputResponse were made to get a feeling for the different responses:
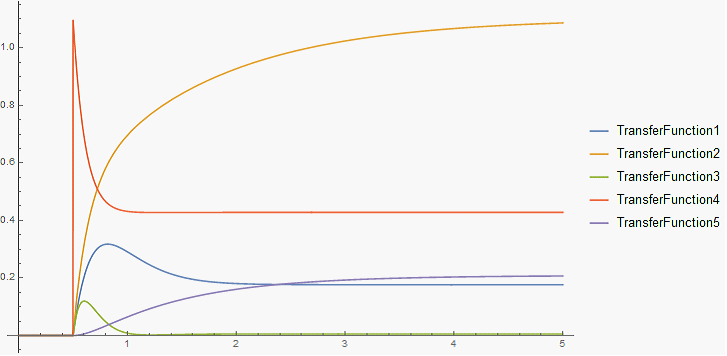
Transfer functions (and state space models) that are created in Mathematica can be imported into SystemModeler using the WSMCreateModel function:
Needs["WSMLink`"]
tf = {
TransferFunctionModel[{{{((2.8 (1.1 + s)) (6. + s)) (9. + s)}}, (((4.5 + s) (5.1 + s)) (5.7 + s)) (7.2 + s)}, s],
TransferFunctionModel[{{{(4.3 (1.5 + s)) (7.1 + s)}}, ((0.8 + s) (5.9 + s)) (8.8 + s)}, s],
TransferFunctionModel[{{{(3.1 (0.2 + s)) (3.3 + s)}}, ((5.1 + s) (8.2 + s)) (9. + s)}, s],
TransferFunctionModel[{{{(1.1 (4.2 + s)) (4.7 + s)}}, (5.9 + s) (8.6 + s)}, s],
TransferFunctionModel[{{{(1.4 (3.2 + s)) (5.6 + s)}}, (((1.1 + s) (3.5 + s)) (5.2 + s)) (6. + s)}, s]};
Table[WSMCreateModel["PlantControl.Blocks.TransferFunction" <> ToString[i], tf[[i]]], {i,1, Length[tf]}]
The components where connected together in SystemModeler and the total system response was set to be the sum of the individual transfer function responses, as mentioned earlier:
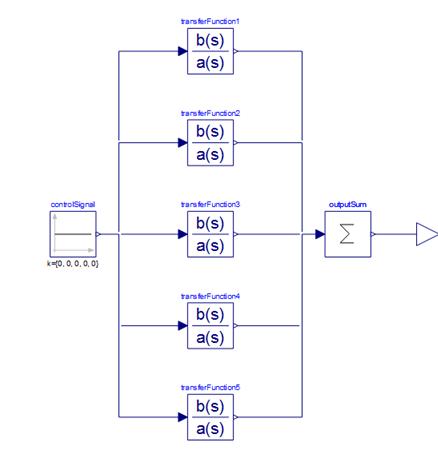
The connections could also have been made directly from Mathematica using the WSMConnectComponents function.
As the models are written in Modelica, we are of course not limited to simple block based models like these. Mechanical, electrical, thermal and/or, biochemical models are all a possibility. The free SystemDynamics library could also be a prime candidate. Neither do the models have to be linear, they can be nonlinear or hybrid. For the sake of simplicity and generality I will stick with my system of transfer functions! I do however invite the community to try out more specific areas of application.
In Mathematica, a ScheduledTaskObject can be created so that, at each update instant the model is simulated using the newest available values and the predicted responses are stored together with the latest measured response. Two separate predictions were made, one (mainPrediction) predicted the system response based on the current estimated state and the current control signals, while the other used user defined control signals (testPrediction).
As the system presented here is purely fictitious, the values could not be gathered "online". Instead the system was excited beforehand using random, piece-wise constant input signals to generate a set of inputs and responses. Some measurement noise was also added to the input and response signals. The "online" part of the process then consisted of collecting these predefined data points, one at a time. For a real process, or a prototype process the signals could be gathered either via Mathematica and sent to the simulation as a parameter, or directly in the process model, for example using the ModelPlug or OPC Modelica libraries. In fact, I would love to try and set up my Arduino board at home doing something like this so if anyone has any ideas or suggestions for a hobby application of this, please let me know!
Anyway, here is the code for the scheduled task:
updateFrequency = 15;
predictionLoop = CreateScheduledTask[
{mainPrediction =
WSMSimulate["PlantControl.ControlModel", {0, predictionLength},
WSMParameterValues -> Join[
Table["controlSignal[" <> ToString[j] <> "].k" -> u[[j, i]], {j, 1,5}],
Table["transferFunction" <> ToString[j] <> ".y_start" -> yindv[[j, i]], {j, 1, 5}]],
Method -> {"DASSL", "InterpolationPoints" -> predictionLength*2}];
testPrediction =
WSMSimulate["PlantControl.ControlModel", {0, predictionLength},
WSMParameterValues -> Join[Table["controlSignal[" <> ToString[j] <> "].k" ->
If[ContainsAny[unlinked, {j}], testInput[[j]], u[[j, i]]], {j, 1, 5}],
Table["transferFunction" <> ToString[j] <> ".y_start" -> yindv[[j, i]], {j, 1, 5}]],
Method -> {"DASSL",
"InterpolationPoints" -> predictionLength*2}];
mainPredictionData[[All, 2]] = Join[
mainPredictionData[[2 ;; historyLength + 1, 2]], mainPrediction["y", Range[0, predictionLength]]];
testPredictionData[[All, 2]] = testPrediction["y", Range[0, predictionLength]];
historyData[[All, 2]] = Append[historyData[[2 ;; -1, 2]], y[[i]]];
i++;}, {updateFrequency, Length[y] - 1}];
Also included is an interface using dynamically updated cells and plots. By clicking on the "link" button you link or unlink the input signals to and from the "actual" process values, allowing you to specify your own input values. If all input values are linked to the process values, the "test prediction" and the "main prediction" will be the same. Here is an image of the control panel and plot:
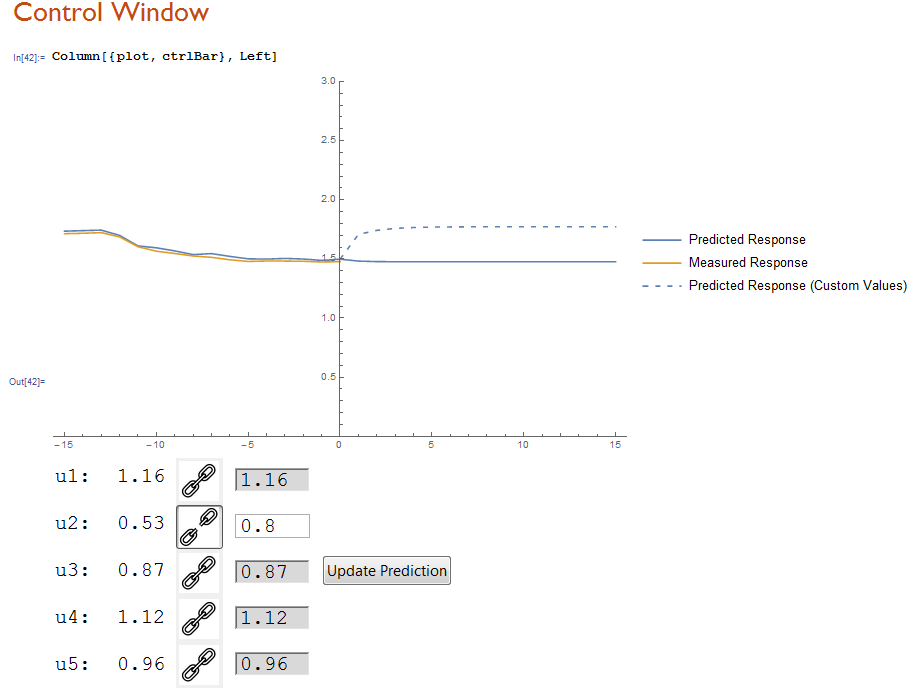
You can download the Notebook and model below and try it for yourself!
If anyone is interested, here are some ideas how this could be expanded:
- Application to a more realistic scenario. A good place to start could be the SystemDynamics library which contains some great examples that could be used for this purpose.
- The input signals specified by the user are simulated as being constant for the duration of the prediction. An alternative approach would be to use, for example, a delayed step between the current and new input value, a ramp or pulses. You can change the nature of the input signal by changing the corresponding block in the simulation model. Maybe the user could be allowed to choose from a number of different signal types from a drop down menu in Mathematica?
- Replace the fictitious signals with real online signals from for example the ModelPlug Modelica library or maybe by connecting over TCP/IP using Mathematica!
 Attachments:
Attachments: