Hi Doug,
I've been testing myself. Here is the new code:
Manipulate[
{
PasteButton["Get values",{1-saturation-offset, b(1-saturation-offset)}],
(image=ImageData[RandomImage[{saturation+offset,1.0},{100,100},ColorSpace->"RGB"]];
ImageCompose[Image[image,ImageSize->200],
Image[Partition[Transpose[{r,g,b}*Transpose[Flatten[image[[25;;75,25;;75,All]],1]]],50],ImageSize->200]])
},
{{offset,0},.05,-.05},{{saturation,0.5},.95,0.05},{{r,1.0},0.0,1.0},{{g,1.0},.85,1.0},{{b,1.0},.85,1.0}
]
To make the sliders less sensitive, I added a finer Saturation control. This isn't strictly necessary, because pressing the alt key while moving the sliders increases their sensitivity by 10. But that's an esoteric feature some might not know.
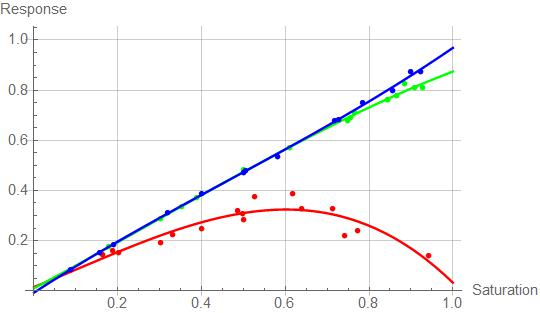
The response is taken as the red slider, say, multiplied by the saturation being tested. In the cases of the green and blue, this makes the response almost equal to the stimulus. But for the red, things are very different.
There is also a PasteButton[], which sends the values of the test datum to the current output position in the notebook. These form a series of lists, but commas and surrounding braces need to be added to finish them off.
The values are fitted to a third order polynomial. Here the blue values are fitted:
xxxb=Fit[valsb,{1,x,x^2,x^3},x]
The whole set of data points and fitted functions look like this:
Show[
ListPlot[valsr, PlotStyle -> Red],
Plot[eqnr[x], {x, 0, 1}, PlotStyle -> Red],
Plot[eqng[x], {x, 0, 1}, PlotStyle -> Green],
ListPlot[valsg, PlotStyle -> Green],
ListPlot[valsb, PlotStyle -> Blue],
Plot[eqnb[x], {x, 0, 1}, PlotStyle -> Blue],
PlotRange -> {{0, 1}, {0, 1}}, AxesOrigin -> {0, 0},
AxesLabel -> {Saturation, Response}
]
Eric