ClearAll["Global`*"]
speed = 10 Quantity[1, ("Miles")/("Hours")] ;(*Speed of Car *)
period = 10 Quantity[1, "Feet"];(* Period of peaks*)
ampl = Quantity[.3, "Feet"] ;(*Half peak Amplitude*)
ampl
Subscript[\[Omega], b] = \!\(TraditionalForm\`
\*FractionBox[\(2\ \[Pi]\ speed\), \(period\)]\);
yy[t_] :=
ampl*Sin[(2 \[Pi] speed t)/( 2 period)]^11 UnitStep[t/
Quantity[1, "Seconds"]] -
ampl Sin[(2 \[Pi] speed t)/( 2 period)]^11 UnitStep[
t/Quantity[1, "Seconds"] - 4]; Plot[
Evaluate[yy[t]], {t, 0 Quantity[0, "Seconds"],
4.5 Quantity[1, "Seconds"]}, PlotTheme -> "Web",
FrameLabel -> Automatic]
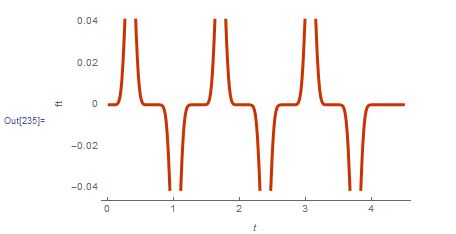
Why is the Plotted amplitude not .3 ft (if ampl = .3 ft)?
am I missing something with the units ? or UnitStep function ?
Kind regards,
John