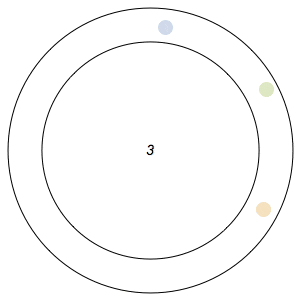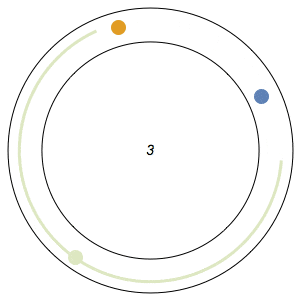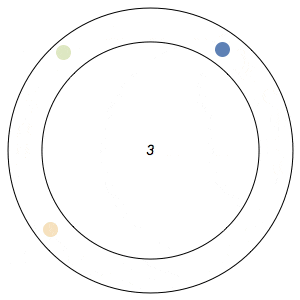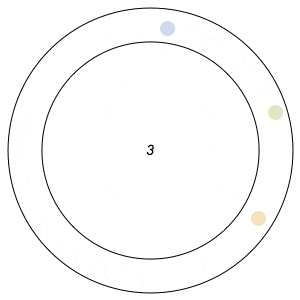
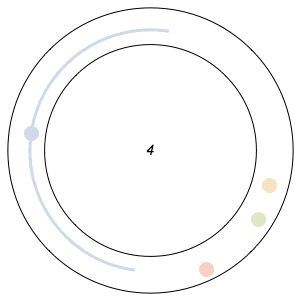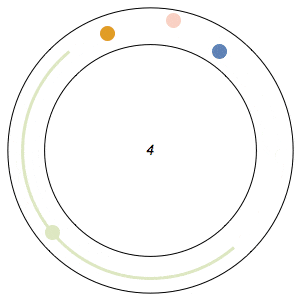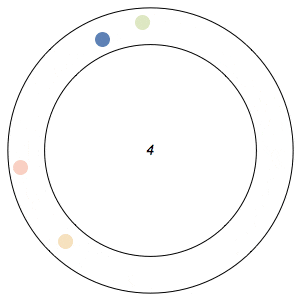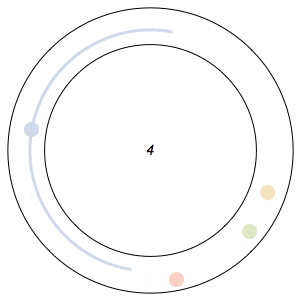
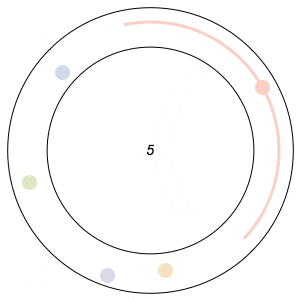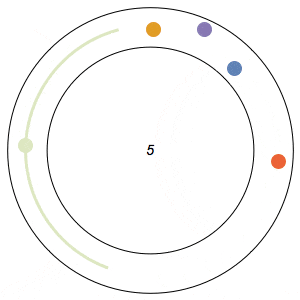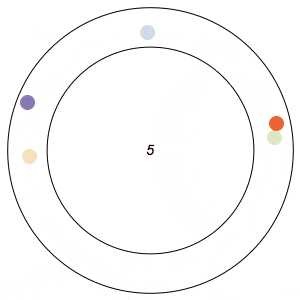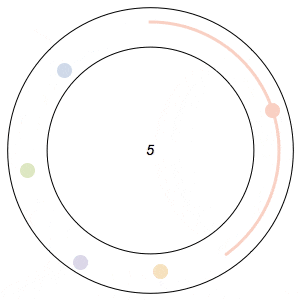
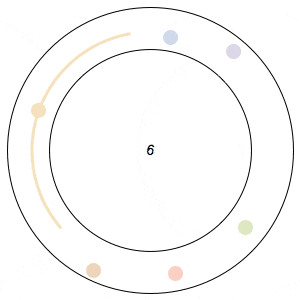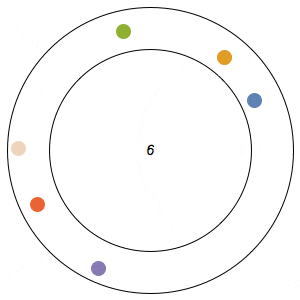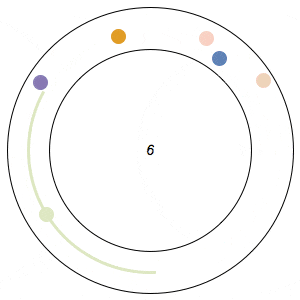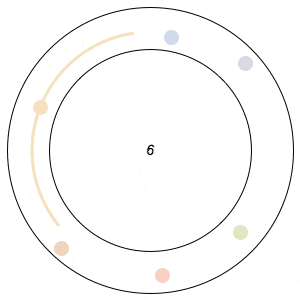
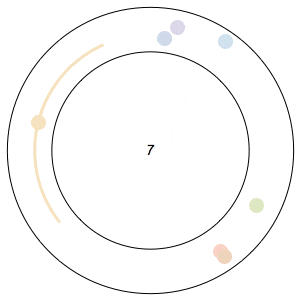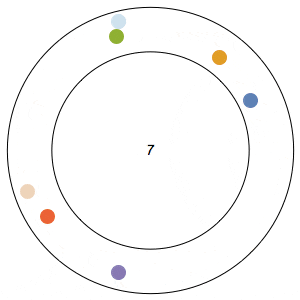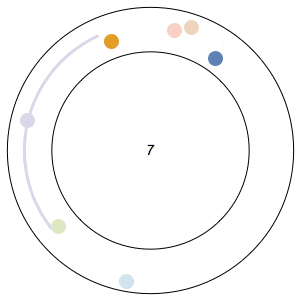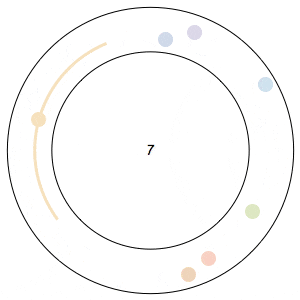
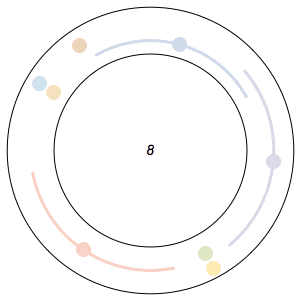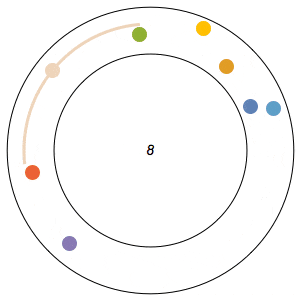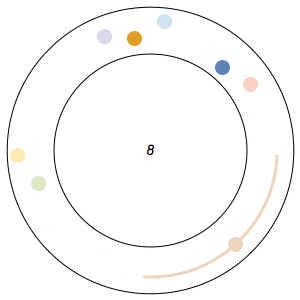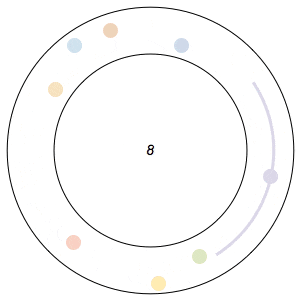
Imagine n runners on a circular track of length 1. The runners start from the same spot at the same time, and each has a distinct, constant speed. A runner is considered “lonely” whenever it is a distance of at least 1/n from every other runner. The Lonely Runner Conjecture (LRC) states that each runner will eventually, at some point in time, be lonely.

Said differently, the LRC states that for each runner, the spacing around it will eventually be greater than or equal to the spacing it would experience if the all of the runners were equally distributed around the track.

The conjecture has been proven to be true for 7 or fewer runners, but, interestingly enough, has never been proven to work for all cases of 8 or more runners. In my 8-runner simulation above, I’ve only shown that it works for a specific set of runner speeds — I haven’t proven that it works for all sets of speeds.

In the GIFs above, an arc appears around a runner whenever the runner is lonely, and the color of a runner fades after it’s been lonely at least once.

More references:

• The lonely runner with seven runners
• The Lonely Runner Conjecture
• The lonely runner conjecture

Originally posted on Fouriest Series.

circ = 1; rad = circ/(2 \[Pi]); nRunners = 5;
rList[t_] := {1 t, 2 t, 4 t, 8 t, 9.6 t, 21 t, 31 t, 33 t}[[1 ;; nRunners]]

dist[d\[Theta]_, circ_] := 
  N[circ/2 (TriangleWave[(d\[Theta] - \[Pi]/2)/(2 \[Pi])] + 1)/2]
minDist[runnerList_, circ_] :=
 Table[
  runner = runnerList[[i]];
  other = DeleteCases[runnerList, runner];
  Min[dist[Abs[runner - other], circ]],
  {i, 1, nRunners}
  ]

colorList = Table[ColorData[97, "ColorList"][[i]], {i, 1, 10}];
colorListLighter = Table[Lighter[ColorData[97, "ColorList"][[i]], 0.7], {i, 1, 10}];

Manipulate[
 {Graphics[
    {
     White, EdgeForm[Black],
     Disk[{0, 0}, rad + 0.005 (nRunners + 3)],
     Disk[{0, 0}, rad - 0.005*3],
     Table[
      {
       If[(minDist[rList[tmax], circ][[i]]) >= 1/nRunners,
        colorList[[i]] = colorListLighter[[i]],
        White
        ],
       Thickness[0.01], 
       Circle[{0, 0}, 
        rad + 0.005 i, {rList[tmax][[i]] - (2 \[Pi])/nRunners, 
         rList[tmax][[i]] + (2 \[Pi])/nRunners}]
       }
      , {i, 1, nRunners}
      ],
     Table[
      {
       If[(minDist[rList[tmax], circ][[i]]) >= 1/nRunners,
        colorList[[i]] = colorListLighter[[i]],
        colorList[[i]]
        ], PointSize[0.05], 
       Point[(rad + 0.005 i) {Cos[rList[tmax][[i]]], 
          Sin[rList[tmax][[i]]]}]
       }
      , {i, 1, nRunners}
      ],
     {Black, Text[Style[ToString[nRunners], 14, Italic], {0, 0}]}
     },
    PlotRange -> rad + 0.005 (nRunners + 3) + 0.01
    ]}[[1]],
 {tmax, 0.00001, 3, .00001}]