Fresh start of Win 7 MMA 10 notebook.
In[1]:= f[sj_] := -1. - (1000. E^(1. (2. - (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)])/sj)))/(2.71828 +
E^(1. (2. - (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)])/sj)))+(1000. E^(1. (2. - (1. + 1. sj +
1. sj ProductLog[E^(-1. - 1./sj)])/sj)) (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)]))/(2.71828 +
E^(1. (2. - (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)])/sj)));
FindRoot[f[sj], {sj, .2}]
During evaluation of In[1]:= FindRoot::lstol: The line search decreased the step size to within tolerance
specified by AccuracyGoal and PrecisionGoal but was unable to find a sufficient decrease in the merit
function. You may need more than MachinePrecision digits of working precision to meet these tolerances. >>
Out[2]= {sj -> 0.0172505}
In[3]:= Plot[f[sj], {sj, 0, .3}]
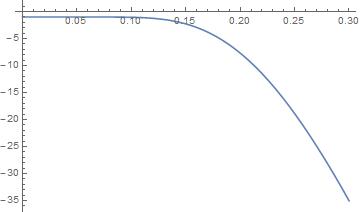
Hummm... Evaluation->quit kernel->local->quit
Now, instead of defining that function, paste that identical expression inside FindRoot and Plot
In[1]:= FindRoot[-1. - (1000. E^(1. (2. - (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)])/sj)))/(2.71828 +
E^(1. (2. - (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)])/sj))) + (1000. E^(1. (2. - (1. + 1. sj +
1. sj ProductLog[E^(-1. - 1./sj)])/sj)) (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)]))/(2.71828 +
E^(1. (2. - (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)])/sj))), {sj, .2}]
Out[1]= {sj -> 0.190651}
In[2]:= Plot[-1. - (1000. E^(1. (2. - (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)])/sj)))/(2.71828 +
E^(1. (2. - (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)])/sj))) + (1000. E^(1. (2. - (1. + 1. sj +
1. sj ProductLog[E^(-1. - 1./sj)])/sj)) (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)]))/(2.71828 +
E^(1. (2. - (1. + 1. sj + 1. sj ProductLog[E^(-1. - 1./sj)])/sj))), {sj, 0, .3}]
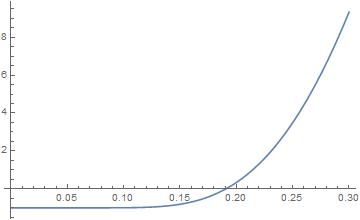
That seems unexpected to me.
This seems to make the problem go away
In[1]:= f[sj_] := FullSimplify[Rationalize[...]];
FindRoot[f[sj], {sj, .2}]
Out[2]= {sj -> 0.190651}