Thank you for opening this thread. I am a university student.
Could anyone help me to calculate the following summation numerically under a certain precision?

This is an expansion of Harmonic Number by introducing the parameter m. Setting m=1 implies
HarmonicNumber[n].
PROBLEM:
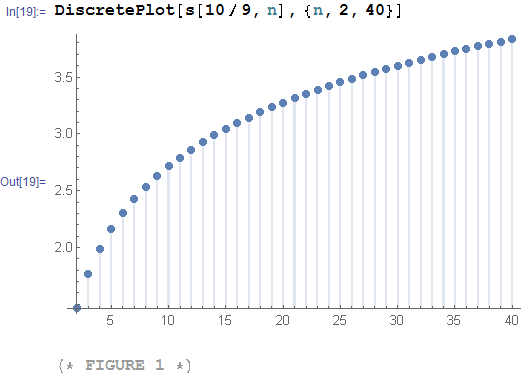
If n is not so big, e.g., n<=40, I can obtain the correct results with m=10/9 (see, Figure 1).
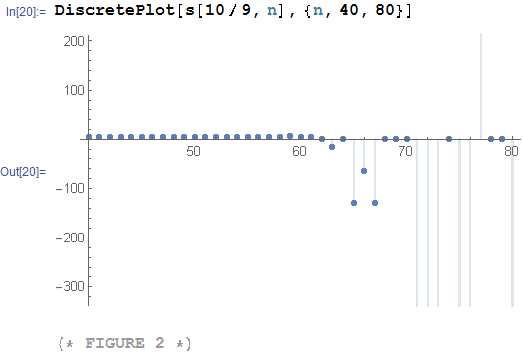
But when n goes to large, the numerical results behave not stable (see, Figure 2).
How can I avoid this abnormal results technically? Actually I need to calculate the case of n=100 and m>1.
Thank you in advance.