Hi. I would like to construct sparse matrix with 9 diagonals. It is organized as 4 blocks with 3 diagonals each. Something like this: (A B);(C D) Currently, I am using For loop for the job, but I suspect there is a more efficient way. My code is:
Agornja[z_] := z*agornja;
Aglavna[z_] := z*aglavna;
Adonja[z_] := z*adonja;
Bgornja[z_] := z*bgornja;
Bglavna[z_] := z*bglavna;
Bdonja[z_] := z*bdonja;
Cgornja[z_] := z*cgornja;
Cglavna[z_] := z*cglavna;
Cdonja[z_] := z*cdonja;
Dgornja[z_] := z*dgornja;
Dglavna[z_] := z*dglavna;
Ddonja[z_] := z*ddonja;
Where z is just for me to see the incrementation. For loop is:
brojelemenata = 10;
korak = 1;
pocetnatacka = 1;
z = pocetnatacka - korak;
elementi[prvi_, drugi_] = 0;
HC = Array[elementi, {brojelemenata, brojelemenata}];
For[i = 1, i < brojelemenata/2, i++,
HC[[i, i]] = Aglavna[z + i*korak];
HC[[i, i + 1]] = Agornja[z + (i + 1)*korak];
HC[[i + 1, i]] = Adonja[z + i*korak];
If[i + brojelemenata/2 + 1 <= brojelemenata,
HC[[i + brojelemenata/2, i + brojelemenata/2]] =
Dglavna[z + i*korak];
HC[[i + brojelemenata/2, i + brojelemenata/2 + 1]] =
Dgornja[z + (i + 1)*korak];
HC[[i + brojelemenata/2 + 1, i + brojelemenata/2]] =
Ddonja[z + i*korak];
If[i + brojelemenata/2 + 1 <= brojelemenata,
HC[[i, i + brojelemenata/2]] = Bglavna[z + i*korak];
HC[[i + 1, i + brojelemenata/2]] = Bdonja[z + i*korak];
HC[[i, i + brojelemenata/2 + 1]] = Bgornja[z + (i + 1)*korak];
HC[[i + brojelemenata/2, i]] = Cglavna[z + i*korak];
HC[[i + brojelemenata/2, i + 1]] = Cgornja[z + (i + 1)*korak];
HC[[i + brojelemenata/2 + 1, i]] = Cdonja[z + i*korak];
];
];
];
HC[[brojelemenata/2, brojelemenata/2]] =
Aglavna[z + korak*brojelemenata/2];
HC[[1, brojelemenata/2]] = 0;
HC[[brojelemenata/2, 1]] = 0;
HC[[brojelemenata/2, brojelemenata]] =
Bglavna[z + korak*brojelemenata/2];
HC[[brojelemenata, brojelemenata/2]] =
Cglavna[z + korak*brojelemenata/2];
HC[[brojelemenata, brojelemenata]] =
Dglavna[z + korak*brojelemenata/2];
HC // MatrixForm
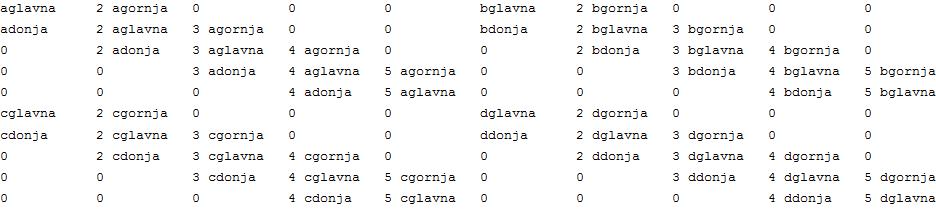
Where first 4 lines are number of elements; step; starting point; and z0. The matrix should look like: