Group Abstract Group Abstract

Message Boards Message Boards

0
|
4.7K Views
|
3 Replies
|
0 Total Likes
View groups...
Share
Share this post:

Inverting, multiplication, equations with complex matrices?

Grzegorz Pilat, Student
Posted 10 years ago

Hello. I'm a student of Electrical Engineering. I would like to use Wolfram as a complex matrices equations calculator.

Wolfram make great job with that type of equations:

(inv {{8-8i, -2-2i, 4}, {8-41i, -2-12i, 54}, {5-8i, -51-2i, 12}})*({{-12}, {11}, { 3}})=({{x}, {y}, { z}})

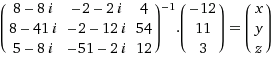
Wolfram make great job with that type of equations

Problem appears when I'm trying to place complex numbers to second matrice:

(inv {{8-8i, -2-2i, 4}, {8-41i, -2-12i, 54}, {5-8i, -51-2i, 12}})*({{-12+13i}, {11+2i}, { 3+4i}})=({{x}, {y}, { z}})

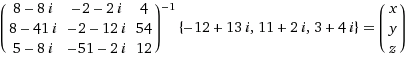
enter image description here

It looks like, wolfram doesn't treat this

({{-12+13i}, {11+2i}, { 3+4i}})

as a matrix. THE QUESTION IS: Am I doing something wrong, or Wolfram doesn't support that kind of calculation? Thank you in advance, Gregory
POSTED BY: Grzegorz Pilat
3 Replies
Sort By:

Thanks, but it didn't help me.

As I wrote, the problem appears when I place complex numbers to the matrix, that you named as B.

I want to multiply two matrices that, both contain complex numbers.
POSTED BY: Grzegorz Pilat
Okkes Dulgerci
Okkes Dulgerci
Posted 10 years ago 
A = {{8 - 8 I, -2 - 2 I, 4}, {8 - 41 I, -2 - 12 I, 
    54}, {5 - 8 I, -51 - 2 I, 12}};
b = {{-12 + 13 I}, {11 + 2 I}, {3 + 4 I}};

Inverse[A].b
POSTED BY: Okkes Dulgerci
Okkes Dulgerci
Okkes Dulgerci
Posted 10 years ago 
A = {{8 - 8 I, -2 - 2 I, 4}, {8 - 41 I, -2 - 12 I,  54}, {5 - 8 I, -51 - 2 I, 12}};
b = {{-12}, {11}, {3}};

Inverse[A].b
POSTED BY: Okkes Dulgerci
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard