I will use this potential to calculate some physical properties
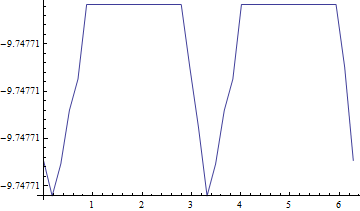
to do so, I need to find a fitting function. The series expansion
a0+Cos[x] a1+Cos[x]^2 a2+Cos[x]^3 a3+Cos[x]^4 a4+Cos[x]^5 a5+b0+Sin[x] b1+Sin[x]^2 b2+Sin[x]^3 b3+Sin[x]^4 b4+Sin[x]^5 b5
truncated at the 5th degree gives the following fitting
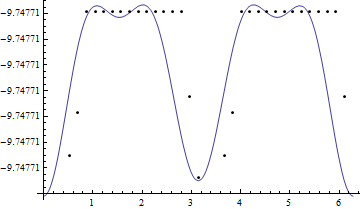
Which could serve the purpose except that periodicity disappears at the beginning of the curve: the well becomes deeper than what it should be. How can I enforce periodicity on the fitting function?