Message Boards Message Boards

1
|
4397 Views
|
3 Replies
|
2 Total Likes
View groups...
Share
Share this post:

Command substitute of ListSurfaceOfRevolucion

Luis Ledesma
Posted 9 years ago

Hello everyone,

after reviewing some notes that I have I did with previous versions of Mathematica, I ask for the ListSurfaceOfRevolucion command because I was very useful to understand more about solids of revolution, but unfortunately no longer exists in version 10 mathematica, so turn to this community to ask if anyone knows the command which replaced ListSurfaceOfRevolucion this because they think occupy again to help other students with the theme of solids of revolution.

I share some images that I could rescue some ideas I had, I hope they serve to understand what I'm looking and someone can help me. Greetings and thanks in advance.

bottom

front

top

Here is the points I used.

points
POSTED BY: Luis Ledesma
3 Replies
Sort By:
Luis Ledesma
Luis Ledesma
Posted 9 years ago

Thank you very much for your help Sanders, that's exactly what I was looking for, I think this will be very helpful to several acquaintances, besides this as more people see it get better, but I sincerely not believe that there is much room for improvement. Thanks for your help, saludos amigo.

Luis Ledesma
POSTED BY: Luis Ledesma

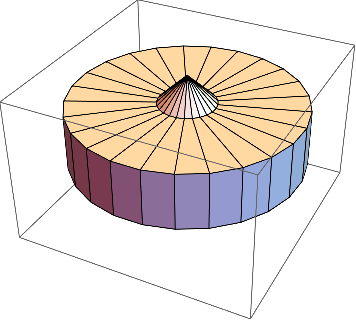
Even better is redoing what they did:

ClearAll[ListRevolutionPlot3D]
ListRevolutionPlot3D[rzpts_List,\[Theta]n_Integer?Positive]:=Module[{\[Theta],pts,indices,dims},
    \[Theta]=CirclePoints[\[Theta]n];
    pts=Table[Append[rz[[1]] j,rz[[2]]],{rz,rzpts},{j,\[Theta]}];
    dims=Most[Dimensions[pts]];
    pts=Join@@pts;
    indices=ArrayReshape[Range[Times@@dims],dims];
    indices=Partition[indices,{2,2},{1,1},{1,1}];
    indices=Map[Flatten[#][[{1,2,4,3}]]&,indices,{2}];
    Graphics3D[GraphicsComplex[pts,Map[Polygon,indices,{2}]]]
]

pts={{0,0},{1,1},{2,1},{2,2},{0.5,2},{0,2.5}}
ListRevolutionPlot3D[pts,25]

enter image description here
POSTED BY: Sander Huisman

Perhaps a solution that works something like this:

pts = {{0, 0}, {1, 1}, {2, 1}, {2, 2}, {0.5, 2}, {0, 2.5}}
{f1, f2} = Interpolation[#, InterpolationOrder -> 1] & /@ Transpose[pts]
RevolutionPlot3D[{f1[t], f2[t]}, {t, 1, 6}, PlotPoints -> 80, MaxRecursion -> 0]

¡saludos! --SH
POSTED BY: Sander Huisman
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract