Hi guys -
Wolfram Demonstrations has a nice interactive model of mortal Fibonacci rabbits here:
http://demonstrations.wolfram.com/MortalFibonacciRabbits/
I've been trying to play with the function used to generate the number of rabbits in some generation n when the rabbits die in month n. I used the summation indicated in the paper that Oleksander links. Here's the code I use:
m := 19;
wabbits[0] = 0;
wabbits[1] = 1;
wabbits[2] = 1;
wabbits[3] = 2;
wabbits[n_] := wabbits[n] = \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = \((n - m)\)\), \(n -
2\)]\(wabbits[k]\)\)
For small n and m it works nicely. (Try n=6, m=3).
But for larger numbers, such as m= 19 and n=90, I start running into trouble.
For example, try m=15, n=33:

With even larger values, for example n=70 and m=19 it tells me I'm exceeding the recursion depth:
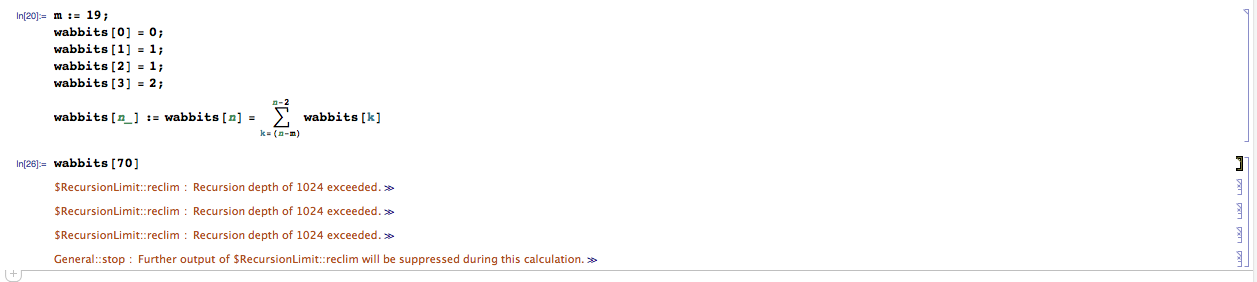
I know this should have an actual, computable value (ROSALIND has a problem to that effect, with n up to 100 and m up to 20; problem code: fibd).
Is the problem with my function definition? Do I have to add anything to make this work for larger numbers? I already added the part
wabbits[n_]:=wabbits[n]
to save on recursion operations needed to compute large values. The demonstration project uses an even more complicated function which can take variations in fertility month and starting pairs into account, working just fine.