In general, when Mathematica just returns your input, perhaps with very tiny changes but not providing a solution, that is code telling you that it has no idea how to solve that particular problem.
Lots, maybe even almost all, differential equations do not have nice simple closed form symbolic solutions.
A good idea when one problem doesn't work is to try a very simple problem where you know the solution. For example:
DSolve[{f''[t] == -f[t], f[0] == 0, f'[0] == 1}, f[t], t]
should return
{{f[t] -> Sin[t]}}
If that works then you should have a tiny bit more confidence that your Mathematica appears to be functioning.
Or for your original problem you can assign constant values to all the parameters and try to get a numerical solution.
a = -1; c = 2; d = 3;
sols = NDSolve[{f''[t]^2+f'[t]^2 (12 c+24 c d Exp[a f[t]])+d Exp[a f[t]] (2 a+a^2 d Exp[a f[t]])==0, f[0]==0, f'[0]==1}, f[t], {t,0,1}]
That will complain about the solution blowing up, but it is possible to see some information before it blows up.
sol1 = f[t] /. sols[[1]];
sol2 = f[t] /. sols[[2]];
g1 = Plot[{Re[sol1], Im[sol1]}, {t, 0, 1}]
g2 = Plot[{Re[sol2], Im[sol2]}, {t, 0, 1}]
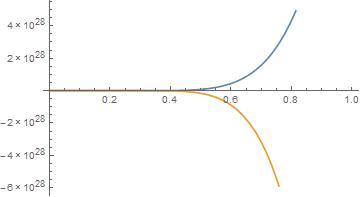
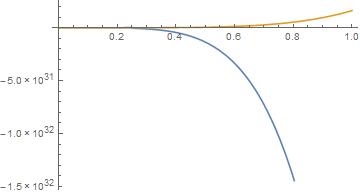
and you might understand why a numerical solver could have a problem finding solutions when the function blows up that quickly.