Hi everyone,
I joined Wolfram's Partnership group a month ago and I was encouraged to make a community post to share some of the interesting programs that I have written while learning the Wolfram language (WL).
In the office that I am in, there's a box titled One Tough Puzzle:

The box contains 9 puzzle pieces:









These puzzles pieces are supposed to interconnect to form a 3x3 grid. I thought that I should solve this puzzle using WL as a way to learn more about WL. In this post, I will describe how I have used WL while I was looking at the problem. The attached notebook has way more detail, my thought process, additional commentary and the fully runnable code (it takes only a few seconds to run).
First, I had to labeled the pieces (it looks a lot nicer in the notebook since \[_____Suit] are actually symbols):
allPieces = <|
"p1" -> {\[SpadeSuit], \[ClubSuit], \[HeartSuit], \[SpadeSuit]},
"p2" -> {\[SpadeSuit], \[HeartSuit], \[ClubSuit], \[HeartSuit]},
"p3" -> {\[DiamondSuit], \[HeartSuit], \[HeartSuit], \
\[DiamondSuit]},
"p4" -> {\[ClubSuit], \[ClubSuit], \[HeartSuit], \[DiamondSuit]},
"p5" -> {\[HeartSuit], \[DiamondSuit], \[SpadeSuit], \
\[DiamondSuit]},
"p6" -> {\[DiamondSuit], \[ClubSuit], \[ClubSuit], \[HeartSuit]},
"p7" -> {\[ClubSuit], \[DiamondSuit], \[DiamondSuit], \[ClubSuit]},
"p8" -> {\[HeartSuit], \[ClubSuit], \[SpadeSuit], \[SpadeSuit]},
"p9" -> {\[SpadeSuit], \[HeartSuit], \[SpadeSuit], \[DiamondSuit]}|>;
From there, I was able to enumerate all the possible connections and made a directed graph:
connectGraph = Graph[Flatten[connectData], VertexLabels -> "Name"]
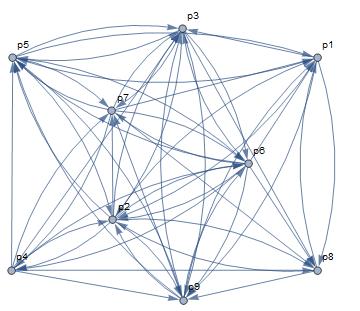
A few other graph theoretic properties were investigated, but there weren't sufficient information to really get to the answer.
Giving it some thoughts, the next step is to reduce the puzzle to a simpler puzzle. Let's try to just make some 2x2 squares.
all4Perm =
Flatten[(Permutations /@ Subsets[Normal[allPieces], {4}]), 1];
valid4Sets = all4Perm[[
Flatten@(Position[Which[
And[all4Perm[[#, 1, 2, 1]] === all4Perm[[#, 2, 2, 3]],
all4Perm[[#, 2, 2, 2]] === all4Perm[[#, 3, 2, 3]],
all4Perm[[#, 3, 2, 2]] === all4Perm[[#, 4, 2, 4]],
all4Perm[[#, 4, 2, 3]] === all4Perm[[#, 1, 2, 2]]], True,
And[all4Perm[[#, 1, 2, 1]] === all4Perm[[#, 2, 2, 3]],
all4Perm[[#, 2, 2, 2]] === all4Perm[[#, 3, 2, 4]],
all4Perm[[#, 3, 2, 3]] === all4Perm[[#, 4, 2, 1]],
all4Perm[[#, 4, 2, 4]] === all4Perm[[#, 1, 2, 2]]], True,
And[all4Perm[[#, 1, 2, 1]] === all4Perm[[#, 2, 2, 4]],
all4Perm[[#, 2, 2, 3]] === all4Perm[[#, 3, 2, 1]],
all4Perm[[#, 3, 2, 4]] === all4Perm[[#, 4, 2, 1]],
all4Perm[[#, 4, 2, 4]] === all4Perm[[#, 1, 2, 2]]], True,
And[all4Perm[[#, 1, 2, 1]] === all4Perm[[#, 2, 2, 4]],
all4Perm[[#, 2, 2, 3]] === all4Perm[[#, 3, 2, 2]],
all4Perm[[#, 3, 2, 1]] === all4Perm[[#, 4, 2, 4]],
all4Perm[[#, 4, 2, 3]] === all4Perm[[#, 1, 2, 2]]], True,
True, False
] & /@ Range[Length[all4Perm]
], True])
]];
The code simply takes 4 puzzle pieces out of the 9 pieces, and checks if these 4 pieces line up correctly. I admit that this code can certainly be improved significantly in both run-time and clarity. Anyway, with a bit of manipulation, it returned 50 possible 2x2 squares that can be formed. Here's one such example:

Once we have these 2x2 squares, it just a matter of fitting these squares into forming a 3x3 square.
valid4Sqrs = allPossiblePerm[[
Flatten@(Position[Which[
And[
allPossiblePerm[[#, 1, 2]] === allPossiblePerm[[#, 2, 1]],
allPossiblePerm[[#, 1, 3]] === allPossiblePerm[[#, 2, 4]],
allPossiblePerm[[#, 2, 3]] === allPossiblePerm[[#, 3, 2]],
allPossiblePerm[[#, 2, 4]] === allPossiblePerm[[#, 3, 1]],
allPossiblePerm[[#, 3, 1]] === allPossiblePerm[[#, 4, 2]],
allPossiblePerm[[#, 3, 4]] === allPossiblePerm[[#, 4, 3]],
allPossiblePerm[[#, 4, 1]] === allPossiblePerm[[#, 1, 4]],
allPossiblePerm[[#, 4, 2]] === allPossiblePerm[[#, 1, 3]]],
True,
True, False
] & /@ Range[Length[allPossiblePerm]
], True])
]]
This is very similar to the code that generated the 2x2 squares since building a 3x3 from 2x2s is the same mechanism, except it has different criteria. To my surprise (after many logic and syntax errors/fixes), it outputs just one combination!
Before the solution of the puzzle, I want to mentioned that I love solving various kind of mathematical puzzle, anything from a good geometric puzzle, like this one, or a logic puzzle or even open problems like the Collatz conjecture or lonely runner conjecture. WL is a great tool for these type of questions. If you have a puzzle that you think is interesting, let me know. I look forward to doing more of these posts.
Happy puzzling!
Wilson
Spoiler Alert

 Attachments:
Attachments: