Numeric solution.
ClearAll["Global`*"]
f[a_?NumericQ, \[Alpha]_?NumericQ] := NIntegrate[x^3/Sqrt[(1 - x)*(1 - x*a^2*Cos[\[Alpha]]) - 3*a*x*Log[x]], {x, 0, 1}]
for a=1 and alfa=Pi
a = 1;
\[Alpha] = Pi;
f[a, \[Alpha]]
(*0.422834*)
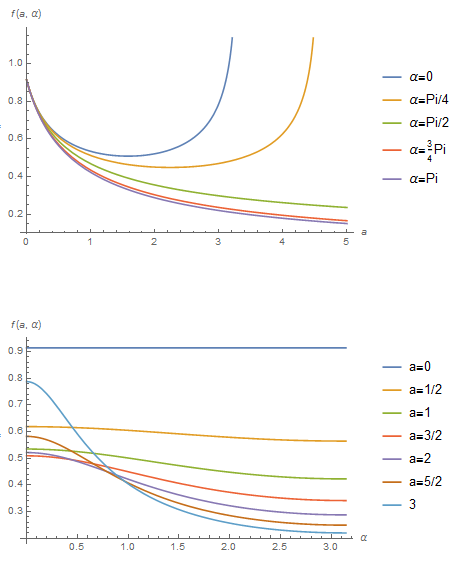
Plot[Evaluate@Table[f[a, \[Alpha]], {\[Alpha], 0, Pi, Pi/4}], {a, 0, 5}, PlotLegends -> {"\[Alpha]=0", "\[Alpha]=Pi/4", "\[Alpha]=Pi/2",
"\[Alpha]=3Pi/4", "\[Alpha]=Pi"}, AxesLabel -> {a, f[a, \[Alpha]]}]
Plot[Evaluate@Table[f[a, \[Alpha]], {a, 0, 3, 1/2}], {\[Alpha], 0, Pi}, PlotLegends -> {"a=0", "a=1/2", "a=1", "a=3/2", "a=2", "a=5/2",
"a=3"}, AxesLabel -> {\[Alpha], f[a, \[Alpha]]}]
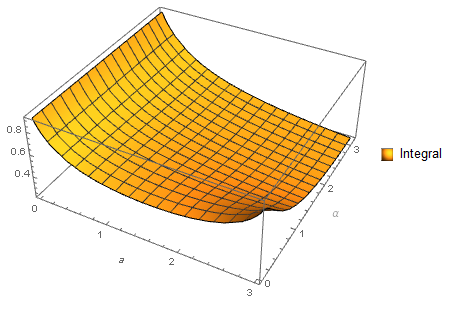
Plot3D[f[a, \[Alpha]], {a, 0, 3}, {\[Alpha], 0, Pi}, AxesLabel -> Automatic, PlotLegends -> {"Integral"}]
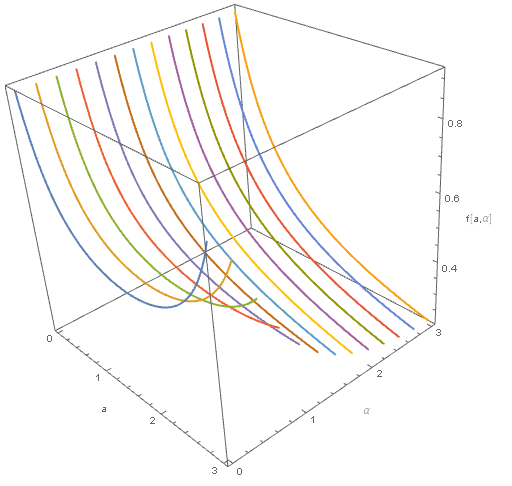
ParametricPlot3D[Evaluate[Table[{a, \[Alpha], f[a, \[Alpha]]}, {\[Alpha], 0, 3, 0.25}]], {a, 0, 3}, BoxRatios -> {1, 1, 1}, AxesLabel -> {"a", "\[Alpha]", "f[a,\[Alpha]]"}]