I've published a package focused on object oriented programming in Mathematica 10.
You can access it on Github at https://github.com/faysou/MTools.
The package is under MIT license. You can fork it and send pull requests.
Short history
I have extracted this package from technology I have been developing over the years for personal projects.
It is based on ideas I started to use in 2010 already. I have been using and debugging the underlying code extensively over the last years. It was difficult (and fun) to develop a project and a language extension at the same time, but the language extension is now relatively stable.
Installation
The package is located here https://github.com/faysou/MTools
Then do:
Needs["MTools`"]
Class declaration
You can declare a new class using the NewClass function which takes optional arguments as input:
TestClass =
NewClass[
"Fields"->
{
"a"->1,"b",
{"c"->3,"PopupMenu","Specs"->{{1,2,3}},"Callback"->((SetProp; Print@#1[#2])&)}
}
,
"Parents"->{GenericClass}
,
"InterfaceOrdering"->{"a","b","c","aa","Id"}
]
Default parameters
This will create a class which constructor has default arguments for the variables "a", "b", "c". The default parameters are stored in
Options@TestClass
In this example "b" will have a None default value. By default all parameters/fields defined in NewClass are stored in an object when it is created. If you don't want this for a given field, you need to put a list around the field declaration, for example {"a"} instead of "a".
Display specification
A display specification is also given as example for "c".
The "Callback" rule in the display specification of "c" takes the following three arguments as input:
#1==object, #2==field, #3==value
SetProp is a shortcut for writing #1.set[#2,#3], ie .for setting a field value in the current object using the value passed by the GUI.
InterfaceOrdering
"InterfaceOrdering" allows to choose which fields to display when an automatic interface generation happens with EditSymbolPane/EditSymbol/InterpretSymbol applied on an object. It can be a list or a matrix. In this example the "Id" field is defined in GenericClass, "aa" is defined in init below.
Super classes
The "Parents" option of NewClass allows to define super classes of the new class. All Classes inherit from the BaseClass class.
Here we use GenericClass as super class.
You can also inherit many classes at the same time (which themselves have super classes) and an appropriate "linearisation" of the inheritance tree will be done similarly to what is explained here.
Init called when an object is created
To further initialize the class you can overload the init function.
TestClass.init[options_]:=
(
o.set["aa",2 o["a"]];
(*how to access an optional parameter if it's not stored*)
o.getOption[options,"a"] // Print;
)
Referring to the current object inside a function
You refer to the current object inside a class function with o (similarly to self in other languages), as shown in the init definition.
Defining a function
To define functions in TestClass you can use the following syntax, which is close from the usual Mathematica syntax for defining functions that use the pattern matcher.
TestClass.function[x_]:= x
Note that the function symbol doesn't need to be exported if used inside a package, as the method resolution will look for the right symbol which also has the "function" name. An exception to this rule is if you give particular attributes to a class function (like HoldAll).
All functions are in fact stored as UpValues, here in TestClass, in the following form
TestClass /: o_TestClass.this.function[x_]:= x
The conversion happens because of an UpValue rule in Dot. This allows to define functions more easily.
Should you wish to add functions to existing classes while developing, or change the signature of class functions, even if objects of these classes already exist you will need to execute
ResetClasses[]
Here are some common operations on an object.
Creating an object
testObject = New[TestClass]["a"->2]
testObject is represented as TestClass[object], where object is a symbol that stores an Association. TestClass has a HoldFirst attribute in order to have a different "object" symbol for each object.
Displaying the properties of an object
PrintSymbol@testObject
Keys@testObject
Values@testObject
Displaying the functions of an object
GetFunctions@testObject
GetArguments@testObject
Getters
testObject["a"]
testObject.a
Setters
testObject.set["a",4]
testObject.a = 4
Function call
testObject.function[2]
Editing an object
InterpretSymbol@testObject
The result of InterpretSymbol is an Interpretation in the Mathematica sense, and can be used the same way you would use testObject. You can execute UninterpretSymbol on the interface to convert it back to a variable name. Note that "c" is displayed using a PopupMenu as specified in the class definition.
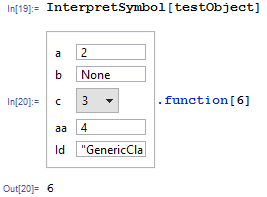
InterpretSymbol and UninterpretSymbol also work directly on a symbol storing an Association.
EditSymbol can be used to edit the properties of an object in a popup, and EditSymbolPane allows to embed the interface corresponding to an object in a bigger interface.
Multiple inheritance
The following example allows to understand how calls to functions work with multiple inheritance.
super allows to call function definitions of super classes.
Also a function can be overloaded in sub classes for all arguments or just some patterns.
In the example below g is overloaded in Y just for even numbers.
X=NewClass["Fields"->{"a"->1}]
X.f[]:=o["a"]
X.g[x_]:=22
Y=NewClass["Parents"->{X}]
Y.f[]:=3
Y.g[x_?EvenQ]:= o.f[]
Z=NewClass["Parents"->{Y}]
Z.f[]:=4
(*Z object definition*)
zz=New[Z]["a"->2]
(*function calls*)
zz.f[] (*defined in Z*)
zz.super.f[] (*defined in Y*)
zz.super[X].f[] (*defined in X*)
zz.g[2] (*defined in Y*)
zz.g[3] (*defined in X*)
The super classes of Z are stored in
Supers[Z] == {X, Y}
This means that when a function from a Z object is executed it will search definitions first in Z, then Y, then X.
Method resolution
It can be interesting to see the intermediate steps to compute zz.g[2] and zz.g[3]
Z[object$1].g[2] ->
defineSub[Z, {object$1}, g, {3}] ->
Y[object$1,Z].this.g[2] ->
Y[object$1,Z].f[] ->
defineSub[Y, {object$1,Z}, f, {}] ->
Z[object$1,Y,Z].this.f[]
Z[object$1].g[3] ->
defineSub[Z, {object$1,Z}, g, {3}] ->
Y[object$1,Z].this.g[3] ->
Y[object$1,Z].super.g[3] ->
X[object$1,Y,Z].this.g[3]
defineSub and super are special functions that search for a function/method definition and cache a search result for all other objects of a given class. They play the role of a dynamic dispatch.
defineSub searches "downward" in the inheritance tree while super searches "upward".
this allows to force the execution to use the definition of a particular class.
Notice a "class stack" after object$1 used in the method resolution when executing definitions in different classes.
In the case of zz.g[2], once the execution happens in Y, the call to f will try to find the "lowest" definition possible, ie. the one corresponding to the least inherited class, which is Z. As Z contains a definition for f, this one will be used.
In the case of zz.g[3], given that g is defined only for even numbers in Y, it would return unevaluated but a special rule added to Y does an automatic call to super in order to find a more general definition in X.
The central part of this project that deals with method resolution is in the MPlusPlus package.
Other syntaxes for defining functions
You can use any pattern in a class function. Note that if you need a function wide condition you would need to put the condition on the rhs.
For example
TestClass.ff[x_]:= x^2 /; Mod[x,3] == 0
You could also use a more lengthy way for defining a function and have the condition on the lhs.
TestClass /: o_TestClass.this.ff[x_] /; Mod[x, 3] == 0 := x^2
Or in some cases where you want a direct access to the object Association in the definition
TestClass /: o:TestClass[object_,___].this.ff[x_] /; Mod[x, 3] == 0 := x^2
Displaying a table with GenericClass and GenericGroup
The following example demonstrates a simple use of GenericClass and GenericGroup to display a table. The columns displayed are configurable and you can nest as many levels as needed.
These two classes can be seen as building block libraries from the package. They allow to do many common operations for managing a tree of objects and displaying them. I refer you to the source code to discover more about them. Almost all of my classes inherit from GenericClass or GenericGroup.
xx=New[GenericClass][];
yy=New[GenericGroup][];
yy.appendComponent[xx];
properties=
{
{"Properties","Editable","Edit","Checkbox",(#.edit[#2]&)},
{"Properties","Color","Color","Property","Default"}
};
yy.registerDisplayedProperties[properties];
yy.set["Color","Pink"];
GenericGroup[].treeDisplay[{yy},"Properties"]

An important function for GenericGroup is iterate, which executes a function on the "Components" of a group object. For example
yy.iterate[get["Id"]]